Конструкции без напряжения арматуры (к СНиП 2.03.01-84), часть 6

• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11
• часть 12
• часть 13
• часть 14
• часть 15
• часть 16
• часть 17
• часть 18
• часть 19
• часть 20

3.42 (3.35). Расчет элементов на действие изгибающего момента для обеспечения прочности по наклонной трещине (черт. 21) должен производиться из условия

(77)

где М — момент от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения, относительно оси, перпендикулярной плоскости действия момента и проходящей через точку приложения равнодействующей усилий N_b в сжатой зоне (черт. 22);

Rs As zs , — S Rsw Asw zsw , S Rsw As,inc zs,inc

сумма моментов относительно той же оси от усилий соответственно в продольной арматуре, хомутах и отгибах, пересекающих растянутую зону наклонного сечения;

z_s , z_sw , z_s,inc — расстояния от плоскостей расположения соответственно продольной арматуры, хомутов и отгибов до указанной оси.

Черт. 21. Схема усилий в наклонном сечении при расчете

его по изгибающему моменту

Высота сжатой зоны наклонного сечения, измеренная по нормали к продольной оси элемента, определяется из условия равновесия проекций усилий в бетоне сжатой зоны и в арматуре, пересекающей наклонное сечение, на продольную ось элемента согласно пп. 3.15 и 3.20. При наличии в элементе отгибов в числитель выражения для х добавляется величина S R_sw A_s,inc cosq (где q — угол наклона отгибов к продольной оси элемента).

Величину z_s допускается принимать равной h ₀  — 0,5х , но при учете сжатой арматуры не более h ₀ – а’ .

Величина S R_sw A_sw z_sw при хомутах постоянной интенсивности определяется по формуле

(78)

где q_sw — усилие в хомутах на единицу длины (см. п. 3.31);

с — длина проекции наклонного сечения на продольную ось элемента, измеренная между точками приложения равнодействующих усилий в растянутой арматуре и сжатой зоне (см. п. 3.45).

Величины z_s,inc для каждой плоскости отгибов определяются по формуле

(79)

где а ₁ — расстояние от начала наклонного сечения до начала отгиба в растянутой зоне (см. черт. 21).

а) б)

Черт. 22. Определение расчетного значения момента

при расчете наклонного сечения

а — для свободно опертой балки; б — для консоли

3.43 (3.35). Расчет наклонных сечений на действие момента производится в местах обрыва или отгиба продольной арматуры, а также у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров.

Кроме того, расчет наклонных сечений на действие момента производится в местах резкого изменения конфигурации элементов (подрезок, узлов и т. п.).

Расчет наклонных сечений на действие момента допускается не производить при выполнении условий (71) и (72) с умножением их правых частей на 0,8 и при значении с не более 0,8c_max .

3.44. При пересечении наклонного сечения с продольной растянутой арматурой, не имеющей анкеров, в пределах зоны анкеровки расчетное сопротивление этой арматуры R_s снижается путем умножения на коэффициент условий работы g _{s 5} , равный:

(80)

где l_x  — расстояние от конца арматуры до точки пересечения наклонного сечения с продольной арматурой;

l_an  — длина зоны анкеровки, определяемая по формуле

(81)

здесь w _an , Dl _an — коэффициенты, принимаемые равными:

для крайних свободных опор балок w _an = 0,5, Dl _an = 8;

для свободных концов консолей w _an = 0,7; Dl _an = 11.

В случае применения гладких стержней коэффициент w _an принимается равным для опор балок и концов консолей соответственно 0,8 и 1,2.

При наличии на крайних свободных опорах косвенной или поперечной арматуры, охватывающей без приваривания продольную арматуру, коэффициент w _an делится на величину 1 +12m _v , а коэффициент Dl _an уменьшается на величину 10s _b /R_b , здесь m _v — объемный коэффициент армирования, определяемый для сварных сеток по формуле (99), для хомутов — по формуле (где A_sw и s — соответственно площадь сечения огибающего хомута и его шаг), в любом случае значение m _v принимается не более 0,06.

Напряжение сжатия бетона на опоре s _b определяется делением опорной реакции на площадь опирания элемента и принимается не более 0,5R_b .

Длина l_an принимается для свободных концов консолей не менее 20d или 250 мм, при этом длину анкеровки l_an можно определить с учетом данных табл. 45 (поз. 1).

В случае приваривания к продольным растянутым стержням поперечной или распределительной арматуры учитываемое в расчете усилие в продольной арматуре R_s А_s увеличивается на величину

(82)

принимаемую не более

В формуле (82):

п_w - число приваренных стержней по длине l_x ;

j _w — коэффициент, принимаемый по табл. 22;

d_w — диаметр приваренных стержней.

Таблица 22

dw	6	8	10	12	14
j w	200	150	120	100	80

Окончательно значение R_s А_s принимается не более значения R_s А_s , определенного без учета g _{s 5} и N_w .

3.45. Для свободно опертых балок невыгоднейшее наклонное сечение начинается от грани опоры и имеет длину проекции с для балок с постоянной высотой сечения, равную:

(83)

но не более максимальной длины приопорного участка, за пределами которого выполняется условие (72) с умножением правой части на 0,8 и при значении с не более 0,8c_max .

В формуле (83):

Q  — поперечная сила в опорном сечении;

F_i , q  — нагрузки соответственно сосредоточенная и равномерно распределенная в пределах наклонного сечения;

A_s,inc — площадь сечения отгибов, пересекающих наклонное сечение;

q — угол наклона отгибов к продольной оси элемента;

q_sw — то же, что в формуле (55).

Если значение с, определенное с учетом сосредоточенной силы F_i , будет меньше расстояния от грани опоры до силы F_i , а определенное без учета силы F_i  — больше этого расстояния, за значение с следует принимать расстояние до силы F_i .

Если в пределах длины с хомуты изменяют свою интенсивность с q_{sw 1} у начала наклонного сечения на q_{sw 2} , значение с определяется по формуле (83) при q_sw = q_{sw 2} и при уменьшении числителя на величину (q_{sw 1} – q_{sw 2} )l ₁ (где l ₁ — длина участка с интенсивностью хомутов q_{sw 1} ).

Для балок, нагруженных равномерно распределенной нагрузкой q , с постоянной интенсивностью хомутов без отгибов условие (77) можно заменить условием

(84)

где Q — поперечная сила в опорном сечении;

М ₀ — момент в сечении по грани опоры.

Для консолей, нагруженных сосредоточенными силами (черт. 22, б ), невыгоднейшее наклонное сечение начинается от мест приложения сосредоточенных сил вблизи свободного конца и имеет длину проекции с для консолей с постоянной высотой, равную:

(85)

но не более расстояния от начала наклонного сечения до опоры (здесь Q ₁ — поперечная сила в начале наклонного сечения).

Для консолей, нагруженных только равномерно распределенной нагрузкой q, невыгоднейшее наклонное сечение заканчивается в опорном сечении и имеет длину проекции с , равную:

(86)

при этом, если с < l – l_an , расчет наклонного сечения можно не производить.

В формуле (86):

А_s  — площадь сечения арматуры, доводимой до свободного конца;

z_{s —} см. п. 3.42; значение z_s определяется для опорного сечения;

l_an — длина зоны анкеровки (см. п. 3.44).

Для элементов с высотой сечения, увеличивающейся с увеличением изгибающего момента, при определении длины проекции невыгоднейшего сечения по формулам (83) или (85) числители этих формул уменьшаются на величину R_s A_s tgb — при наклонной сжатой грани и на величину R_s A_s sinb — при наклонной растянутой грани (где b )  — угол наклона грани к горизонтали) .

3.46. Для обеспечения прочности наклонных сечений на действие изгибающего момента в элементах постоянной высоты с хомутами продольные растянутые стержни, обрываемые в пролете, должны заводиться за точку теоретического обрыва (т. е. за нормальное сечение, в котором внешний момент становится равным несущей способности сечения без учета обрываемых стержней; черт. 23) на длину не менее величины w , определяемой по формуле

(87)

где Q — поперечная сила в нормальном сечении, проходящем через точку теоретического обрыва;

A_s,inc , q — обозначения те же, что в формуле (83);

d  — диаметр обрываемого стержня;

q_sw  — см. п. 3.31.

Для балок с наклонной сжатой гранью числитель формулы (87) уменьшается на R_s A_s tgb , а для балок с наклонной растянутой гранью — на R_s A_s sinb (где b — угол наклона грани к горизонтали). Кроме того, должны быть учтены требования п. 5.44.

Для элементов без поперечной арматуры значение w принимается равным 10d , при этом место теоретического обрыва должно находиться на участке элемента, на котором выполняется условие (72), с умножением правой части на 0,8 и при значении с не более 0,8с_max .

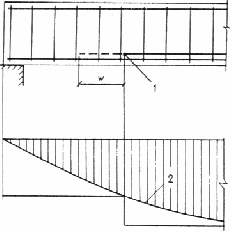
Черт. 23. Обрыв растянутых стержней в пролете

1 — точка теоретического обрыва; 2 — эпюра М

3.47. Для обеспечения прочности наклонных сечений на действие изгибающего момента начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень полностью используется по моменту, не менее чем на h ₀ /2, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб не требуется по расчету.

РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ В ПОДРЕЗКАХ

3.48. Для элементов с резко меняющейся высотой сечения (например, для балок и консолей, имеющих подрезки), производится расчет по поперечной силе для наклонных сечений, проходящих у опоры консоли, образованной подрезкой (черт. 24), согласно пп. 3.31—3.39, при этом в расчетные формулы вводится рабочая высота h ₀₁ короткой консоли, образованной подрезкой.

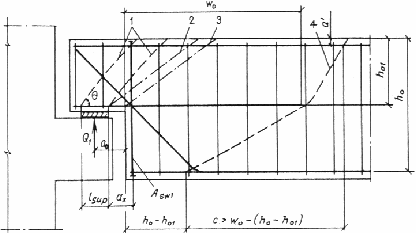
Черт. 24. Невыгоднейшие наклонные сечения

в элементе с подрезкой

1 — наклонная сжатая полоса; 2 — при расчете по поперечной силе; 3 — то же, по изгибающему моменту; 4 — то же, по изгибающему моменту вне подрезки

Хомуты, необходимые для обеспечения прочности наклонного сечения, следует устанавливать за конец подрезки на участке длиной не менее w ₀ , определяемой по формуле (88).

3.49. Для свободно опертых балок с подрезками должен производиться расчет на действие изгибающего момента в наклонном сечении, проходящем через входящий угол подрезки (см. черт. 24), согласно пп. 3.42— 3.45. При этом продольная растянутая арматура в короткой консоли, образованной подрезкой, должна быть заведена за конец подрезки на длину не менее l_an (см. п. 5.44) и не менее величины w ₀ , равной:

(88)

где Q ₁  — поперечная сила в нормальном сечении у конца подрезки;

A_{sw 1}  —площадь сечения дополнительных хомутов, расположенных у конца подрезки на участке длиной не более h ₀₁ /4 и не учитываемых при определении интенсивности хомутов q_sw у подрезки;

A_s,inc — площадь сечения отгибов, проходящих через входящий угол подрезки;

a ₀ — расстояние от опоры консоли до конца подрезки;

d — диаметр обрываемого стержня.

Хомуты и отгибы, установленные у конца подрезки, должны удовлетворять условию

(89)

где h ₀₁ , h ₀  — рабочая высота соответственно в короткой консоли подрезки и в балке вне подрезки.

Если нижняя арматура элемента не имеет анкеров, должна быть также проверена, согласно пп. 3.42—3.45, прочность наклонного сечения, расположенного вне подрезки и начинающегося за указанными хомутами на расстоянии не менее h ₀ — h ₀₁ от торца (см. черт. 24). При этом в расчете не учитывается продольная арматура короткой консоли, а длина проекции с принимается не менее расстояния от начала наклонного сечения до конца указанной арматуры. Кроме того, длина анкеровки l_an для нижней арматуры элемента принимается как для свободных концов консолей.

Расчет короткой консоли подрезки производится согласно пп. 3.99 и 3.100, принимая направление наклонной сжатой полосы от наружного края площадки опирания до равнодействующей усилий в дополнительных хомутах площадью сечения A_{sw 1} на уровне сжатой арматуры балок, т. е. при (где l_sup — см. п. 3.99, a_x — см. черт. 24), при этом в формуле (207) коэффициент 0,8 заменяется на 1,0.

ПРИМЕРЫ РАСЧЕТА

Расчет наклонных сечений на действие поперечной силы

Пример 13. Дано: железобетонная плита перекрытия с размерами поперечного сечения по черт. 25; бетон тяжелый класса В15 (R_b = 7,7 МПа и R_bt = 0,67 МПа при g _{b 2} = 0,9; E_b = 20,5 · 10³ МПа); ребро плиты армировано плоским сварным каркасом с поперечными стержнями из арматуры класса А-III , диаметром 8 мм (A_sw = 50,3 мм² ; R_sw = 285 МПа; E_s = 2 · 10⁵ МПа), шагом s = 100 мм; временная эквивалентная нагрузка v = 18 кН/м; нагрузка от собственного веса плиты и пола g = 3,9 кН/м; поперечная сила на опоре Q_max = 62 кН.

Требуется проверить прочность наклонной полосы ребра между наклонными трещинами, а также прочность наклонных сечений по поперечной силе.

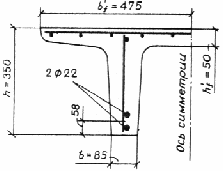
Черт. 25. К примеру расчета 13

Расчет. h ₀ = 350 – 58 = 292 мм. Прочность наклонной полосы проверим из условия (47).

Определим коэффициенты j _{w 1} и j _{b 1} :

отсюда j _{w 1} = 1 + 5am _w = 1 + 5 · 9,76 · 0,0059 = 1,29 < 1,3;

для тяжелого бетона b = 0,01;

тогда

т. е. прочность наклонной полосы обеспечена.

Прочность наклонного сечения по поперечной силе проверим из условия (50).

Определим величины M_b и q_sw :

(см. табл. 21);

так как , принимаем – b = 150 мм, тогда:

Н/мм (кН/м).

Определим значение Q_b,min , принимая j _{b 3} = 0,6:

Поскольку

условие (57) выполняется, и, следовательно, значение М_b не корректируем.

Согласно п. 3.32 определим длину проекции невыгоднейшего наклонного сечения с :

кН/м (Н/мм),

поскольку 0,56q_sw = 0,56 · 143 == 80 кН/м > q ₁ = 12,9 кН/м, значение с определим только по формуле

м.

Тогда

кН.

Длина проекции наклонной трещины равна:

Поскольку c ₀ = 0,288 < h ₀ = 0,292 м, принимаем c ₀ = h ₀ = 0,292 м, тогда Q_sw = q_sw c ₀ = 143 · 0,292 = 41,8 кН.

Проверим условие (50) :

т. е. прочность наклонного сечения по поперечной силе обеспечена. Кроме того, должно выполняться требование п. 3.29:

Условия п. 5.69 s < h /2 = 350/2 = 175 мм и s < 150 мм также выполняются.

Пример 14. Дано: свободно опертая железобетонная балка перекрытия пролетом l = 5,5 м; временная равномерно распределенная эквивалентная нагрузка на балку v = 36 кН/м; постоянная нагрузка g = 14 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм, h ₀ = 370 мм; бетон тяжелый класса В15 (R_b = 7,7 МПа; R_bt = 0,67 МПа при g _{b 2} = 0,9); хомуты из арматуры класса А-I (R_sw = 175 МПа).

Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии от опоры и как может быть увеличен шаг хомутов.

Расчет. Наибольшая поперечная сила в опорном сечении равна:

кН,

где q = v + g = 36 +14 = 50 кН/м.

Определим требуемую интенсивность хомутов приопорного участка согласно п. 3.33 б.

Из формулы (52) при j _f = 0 и j _{b 2} = 2,0 (см. табл. 21) получим

Согласно п. 3.32,

кН/м (Н/мм);

кН.

Так как

интенсивность хомутов определим по формуле (63) :

кН/м (Н/мм).

При этом, поскольку

Н/мм < 130 Н/мм,

оставляем q_sw = 130 Н/мм.

Согласно п. 5.69, шаг s ₁ у опоры должен быть не более h /2 = 200 и 150 мм, а в пролете = 300 и 500 мм. Максимально допустимый шаг у опоры, согласно п. 3.29, равен:

мм.

Принимаем шаг хомутов у опоры s ₁ = 150 мм, а в пролете — 2s ₁ = 300 мм, отсюда

мм² .

Принимаем в поперечном сечении два хомута диаметром по 10 мм (А_sw = 157 мм² ).

Таким образом, принятая интенсивность хомутов у опоры и в пролете балки будет соответственно равна:

Н/мм;

Н/мм.

Проверим условие (57), вычислив Q_b,min :

H.

Тогда

Следовательно, значения q_{sw 1} и q_{sw 2} не корректируем.

Определим, согласно п. 3.34, длину участка l ₁ с интенсивностью хомутов q_{sw 1} . Так как q_{sw 1} — q_{sw 2} = q_{sw 2} = 91,6 H/ мм > q ₁ = 32 Н/мм, значение l ₁ вычислим по формуле

(здесь мм).

Принимаем длину участка с шагом хомутов s ₁ = 150 мм равной 1,64 м.

Пример 15. Дано: железобетонная балка покрытия, нагруженная сосредоточенными силами, как показано на черт. 26, а ; размеры поперечного сечения — по черт. 26, б , бетон тяжелый класса В15 (R_bt = 0,67 МПа при g _{b 2} = 0,9); хомуты из арматуры класса А-I (R_sw = 175 МПа).

Требуется определить диаметр и шаг хомутов, а также выяснить, на каком расстоянии и как может быть увеличен шаг хомутов.

Расчет. Сначала определим, согласно п. 3.31, величину M_b :

(см. табл. 21);

мм (см. черт. 26, б );

мм;

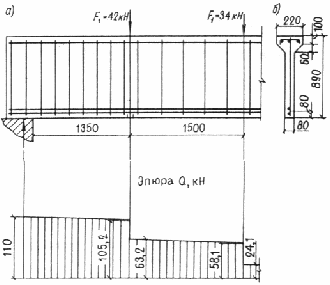
Черт. 26. К примеру расчета 15

Определим требуемую интенсивность хомутов согласно п. 3.33а, принимая длину проекции наклонного сечения с равной расстоянию от опоры до первого груза — с ₁ = 1,35 м.

Поперечная сила на расстоянии с ₁ от опоры равна Q ₁ = 105,2 кН (см. черт. 26).

Из формулы (51) имеем

Тогда

Поскольку с ₁ = 1,35 м < 2 р ₀ = 2 · 0,81 = 1,62 м,

принимаем с ₀ = с ₁ = 1,35 м;

Так как c ₀₁ = 0,417 < c ₁ = 0,667 < с ₁ / с ₀ = 1, значение q_{sw (1)} определим по формуле (59):

кН/м.

Определим q_sw при значении с , равном расстоянию от опоры до второго груза — c ₂ = 2,85 м.

Принимаем Q_{b 2} = Q_b,min = 31,55 кН.

Соответствующая поперечная сила равна Q ₂ = 58,1 кН. Поскольку c ₂ = 2,85 м > 2h ₀ = 1,62 м, принимаем c ₀ = 2h ₀ = 1 ,62 м.

Следовательно, значение q_{sw (2)} определим по формуле (58):

кН/м.

Принимаем максимальное значение q_sw = q_{sw (1)} = 31,18 кН/м.

Из условия сварки (см. п. 5.13) принимаем диаметр хомутов 6 мм (A_sw = 28,3 мм² ), тогда шаг хомутов в приопорном участке равен:

мм.

Принимаем s ₁ = 150 мм. Назначаем шаг хомутов в пролете равным s ₂ = 2s ₁ = 2 · 150 = 300 мм. Длину участка с шагом s ₁ определим из условия обеспечения прочности согласно п. 3.34, при этом

Н/мм;

Н/мм;

Н/мм.

Зададим длину участка с шагом хомутов s ₁ равной расстоянию от опоры до первого груза — l ₁ = 1,35 м; проверим условие (50) при значении с , равном расстоянию от опоры до второго груза — с = 2,85 м > l ₁ . Значение c ₀₁ определим по формуле (56) при q_{sw 1} = 33 кН/м:

Поскольку с – l ₁ = 2,85 —1,35 = 1,5 м < c ₀₁ = 1,6м, значение Q_sw в условии (50) принимаем равным:

кН;

т. е. прочность этого наклонного сечения обеспечена.

Большее значение с не рассматриваем, поскольку при этом поперечная сила резко уменьшается.

Таким образом, длину участка с шагом хомутов s ₁ = 150 мм принимаем равной l ₁ = 1,35м.

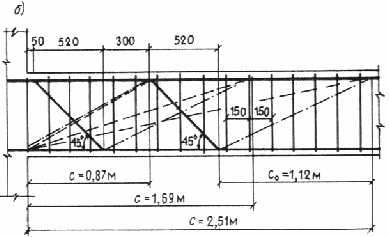
Условные обозначения:

- - - - расчетные наклонные сечения;

-· -· -· - рассматриваемые наклонные трещины

Черт. 27. К примеру расчета 16

Пример 16. Дано: железобетонная балка монолитного перекрытия с размерами поперечного сечения по черт. 27, а ; расположение отогнутых стержней — по черт. 27, б ; временная эквивалентная нагрузка на балку v = 96 кН/м, постоянная — g = 45 кН/м; поперечная сила на опоре Q_max = 380 кН; бетон тяжелый класса В15 (R_bt = 0,67 МПа при g _{b 2} = 0,9); хомуты двухветвевые диаметром 6 мм (A_sw = 57 мм² ) из арматуры класса А-I (R_sw = 175 МПа), шагом s = 150 мм; отогнутые стержни класса А-II (R_sw = 225 МПа), площадью сечения: первой плоскости А_{s,inc 1} = 628 мм² (2 Æ 20), второй — А_{s,inc 2} = 402 мм² (2 Æ 16).

Требуется проверить прочность наклонных сечений по поперечной силе.

Расчет. h ₀ = 600 – 40 = 560 мм. Согласно п. 3.31 находим значения M_b и q_sw :

(см. табл. 21);

мм;

Н/мм.

Согласно п. 3.32 находим q ₁ = g + v /2 = 45 + 96/2 = 93 кН/м.

Проверим из условия (50) с учетом формулы (65) наклонное сечение с длиной проекции, равной расстоянию от опоры до конца второй плоскости отгибов, т. е. при с = 50 + 520 + 300 = 870 мм = 0,87 м.

Поперечная сила на расстоянии с = 0,87 м от опоры равна:

кН.

Определим проекцию опасной наклонной трещины c ₀ согласно п. 3.35.

Сначала определим максимальное значение c ₀ по формуле (56):

принимаем c _0,max = 1,12 м. Поскольку с = 0,87 м < c _0,max = 1,12 м, принимаем для этого наклонного сечения c ₀ = с = 0,87 м. Наклонную трещину, расположенную между концом второй и началом первой плоскостей отгибов, т. е. не пересекающую отгибы, в расчете не рассматриваем, так как для нее c ₀ = 0,30 м < c _0,max .

Для первой плоскости отгибов

Тогда

т. е. прочность данного наклонного сечения обеспечена.

Проверим наклонное сечение, оканчивающееся на расстоянии c ₀ = 1,12 м от начала первой плоскости отгибов, т.е. при с = 0,05 + 0, 52 + 1,12 = 1,69 м.

Поперечная сила на расстоянии с = 1,69 м от опоры равна Q = 380 – 93 · 1,69 = 222,8 кН.

Для второй плоскости отгиба

Для этого сечения принимаем наклонную трещину, проведенную от конца наклонного сечения до начала первой плоскости отгибов, т.е. c ₀ = c _0,max = 1,12 м. Наклонные трещины, проведенные от конца наклонного сечения до опоры и до начала второй плоскости отгибов, не рассматриваем, так как в первом случае c ₀ = с = 1,69 м > c _0,max = 1,12 м, а во втором — трещина не пересекает отгибы при c ₀ < c _0,max .

Тогда

т. е. прочность данного наклонного сечения обеспечена.

Проверим наклонное сечение, оканчивающееся на расстоянии c _0,max = 1, 12 м от начала второй плоскости отгибов, т. е. при с = 0,05 + 0,52 + 0,30 + 0,52 + 1,12 = 2,51 м.

Поперечная сила на расстоянии с = 2,51 м от опоры равна Q = 380 – 93 · 2,51 = 146,6 кН.

Для этого сечения, очевидно, c ₀ = c _0,max = 1,12 м и наклонная трещина отгибы не пересекает, т. е. Q_s,inc = 0. Поскольку c = 2,51 м 1, 87 м, принимаем

Q_b = Q_b,min = 76 ,5 кН

Тогда Q_b + q_sw c ₀ + Q_s,inc = 76,5 + 66,5 · 1,12 + 0 = 151 кН > Q = 146,6 кН, т. е. прочность любых наклонных сечений обеспечена.

Согласно п. 3.29 проверим расстояние между началом первой плоскости отгибов и концом второй плоскости, принимая поперечную силу у конца второй плоскости отгибов Q = 299,1 кН и j _{b 4} = 1,5:

т. е. требование п. 3.29 выполнено.

Пример 17. Дано: железобетонная двускатная балка покрытия пролетом 8,8 м; сплошная равномерно распределенная нагрузка на балку q = 46 кН/м (черт. 28, a ); размеры поперечного сечения — по черт. 28, б ; бетон тяжелый класса В25 (R_bt = 0,95 МПа при g _{b 2} = 0,9); хомуты из арматуры класса А-I (R_sw = 175 МПа), диаметром 8 мм (A_sw = 50,3 мм² ), шагом s = 150 мм.

Требуется проверить прочность наклонных сечений по поперечной силе.

Черт. 28. К примеру расчета 17

Расчет производим согласно п. 3.37.

Рабочая высота опорного сечения равна h ₀₁ = 600 – 80 = 520 мм (черт. 28, б ).

Определим величины j _{f 1} и М_{b 1} по формулам (53) и (52) как для опорного сечения:

мм;

принимаем j _{f 1} = 0,5; j _{b 2} = 2 (см. табл. 21);

По формуле (55) определим величину q_sw :

Н/мм (кН/м).

Определим значение q_inc , принимая tgb = 1/12:

Н/мм (кН/м).

Поскольку нагрузка сплошная, принимаем q ₁ = q = 46 кН/м.

Проверим условие (66):

Условие (66) не выполняется, и, следовательно, значение с вычислим по формуле (68):

при этом c ₀ = с = 0,853 м.

Рабочая высота поперечного сечения h ₀ на расстоянии с = 0,853 м от опоры равна:

м.

Определим величину M_b при h ₀ = 591 мм:

принимаем j _f = 0,5;

Проверим условие (50), принимая поперечную силу в конце наклонного сечения равной:

кН;

т. е. прочность наклонных сечений по поперечной силе обеспечена.

Пример 18. Дано: консоль размерами по черт. 29; сосредоточенная сила на консоли F = 300 кН, расположенная на расстоянии 0,8 м от опоры; бетон тяжелый класса В15 (R_bt = 0,67 МПа при g _{b 2} = 0,9); хомуты двухветвевые диаметром 8 мм (A_sw = 101 мм² ) из арматуры класса А-I (R_sw = 175 МПа), шагом s = 200 мм.

Требуется проверить прочность наклонных сечений по поперечной силе.

Черт. 29. К примеру расчета 18

Расчет. Согласно п. 3.38 проверим из условия (50) наклонное сечение, начинающееся от места приложения сосредоточенной силы, при значении с, определяемом по формуле (68).

Рабочая высота в месте приложения сосредоточенной силы равна мм (см. черт. 29).

По формуле (52) определим величину M_{b 1} , принимая j _{b 2} = 2 (см. табл. 21) и j _f = 0:

Н · мм.

Значение q_sw равно:

Н/мм (кН/м).

Принимая (см. черт. 29), определим q_inc :

Н/мм,

отсюда, принимая q ₁ = 0, имеем

мм,

при этом c ₀ = c = 556 мм.

Поскольку значение с не превышает значения расстояния от груза до опоры, оставим с = 556 мм и определим рабочую высоту h ₀ в конце наклонного сечения:

мм.

Поскольку 2h ₀ = 2 · 510 мм > c ₀ = 558 мм, оставим c ₀ = 556 мм.

Значение M_b равно:

отсюда

т. е. прочность этого наклонного сечения обеспечена.

Для наклонного сечения, располагаемого от груза до опоры, по формуле (56) определим значение c ₀ , принимая h ₀ = 650 – 50 = 600 мм:

Н · мм;

принимаем c ₀ = 2h ₀ = 1200 мм.

Поскольку c ₀ = 1200 мм > с = 800 мм, указанное наклонное сечение можно не проверять. Следовательно, прочность любого наклонного сечения обеспечена.

Пример 19. Дано: сплошная плита перекрытия без поперечной арматуры размером 3х6 м, толщиной h = 160 мм, монолитно связанная по периметру с балками; эквивалентная временная равномерно распределенная нагрузка на плиту v = 50 кН/м² ; нагрузка от собственного веса и пола g = 9 кН/м² ; a = 20 мм; бетон тяжелый класса В25 (R_bt = 0,95 МПа при g _{b 2} = 0,9).

Требуется проверить прочность плиты на действие поперечной силы.

Расчет. h ₀ = h – а = 160 – 20 = 140 мм. Расчет производим для полосы шириной b = 1 м = 1000 мм, пролетом l = 3 м; полная нагрузка на плиту равна q = v + g = 50 + 9 = 59 кН/м.

Поперечная сила на опоре равна:

кН.

Проверим условие (71):

Проверим условие (72). Поскольку боковые края плиты связаны с балками, значение c_max определим с учетом коэффициента a = 1 + 0,05 b/h = 1 + 0,05 · 6/0,16 > 1,25 (здесь b = 6 м — расстояние между боковыми краями плиты), т. е. a = 1,25:

мм.

Согласно п. 3.32 имеем:

(см. табл. 21).

Поскольку 356 Н/мм > q ₁ = 34 Н/мм, принимаем с = c_max = 280 мм = 0,28 м.

Поперечная сила в конце наклонного сечения равна Q = Q_max – q ₁ c = 88,5 – 34 · 0,28 = 79 кН.

т. е. прочность плиты по поперечной силе обеспечена.

Пример 20. Дано: панель резервуара консольного типа с переменной толщиной от 262 (в заделке) до 120 мм (на свободном конце), вылетом 4,25 м; боковое давление грунта, учитывающее нагрузки от транспортных средств на поверхности грунта, линейно убывает от q ₀ = 69 кН/м² в заделке до q = 7 кН/м² на свободном конце; а = 22 мм; бетон тяжелый класса В15 (R_bt = 0,82 МПа при g _{b 2} = 1,1).

Требуется проверить прочность панели по поперечной силе.

Расчет. Рабочая высота сечения панели в заделке равна h ₀₁ = 262 – 22 = 240 мм.

Определим tgb (b  — угол между растянутой и сжатой гранями):

Расчет производим для полосы панели шириной b = 1 м = 1000 мм.

Проверим условия п. 3.40. Поперечная сила в заделке равна:

кН.

Проверим условие (71), принимая h ₀ = h ₀₁ = 240 мм:

т. е. условие выполняется.

Поскольку панели связаны одна с другой, а ширина стенки резервуара заведомо более 5h , значение c_max определим с учетом коэффициента a = 1,25:

мм.

Средняя интенсивность нагрузки на приопорном участке длиной c_max = 464 мм равна q ₁ = 69 – (69 – 7) = 65,6 Н/мм.

Из табл. 21 j _{b 4} =1,5.

Поскольку

= 464 мм, принимаем с = с_max = 464 мм.

Определим рабочую высоту сечения на расстоянии от опоры (т. е. среднее значение h ₀ в пределах длины с ):

мм.

Поперечная сила на расстоянии с == 464 мм от опоры равна:

кН.

Проверим условие (72):

кН,

т. е. прочность панели по поперечной силе обеспечена.

Расчет наклонных сечений на действие изгибающего момента

Пример 21. Дано: свободно опертая железобетонная балка пролетом l = 5,5 м с равномерно распределенной нагрузкой q = 29 кН/м; конструкция приопорного участка балки принята по черт. 30; бетон тяжелый класса В15 (R_b = 7,7 МПа; R_bt = 0,67 МПа при g _{b 2} = 0,9); продольная арматура без анкеров класса А-III (R_s = 365 МПа), площадью сечения A_s = 982 мм² (2 Æ 25) и = 226 мм² (2 Æ 12); хомуты из арматуры класса А-I (R_sw = 175 МПа), диаметром 6 мм, шагом s = 150 мм приварены к продольным стержням.

Требуется проверить прочность наклонных сечений на действие изгибающего момента.

Черт. 30. К примеру расчета 21

Расчет. h ₀ = h – a = 400 – 40 = 360 мм. Поскольку растянутая арматура не имеет анкеров, расчет наклонных сечений на действие момента необходим.

Принимаем начало наклонного сечения у грани опоры. Отсюда l_x = l_sup – 10 мм = 280 – 10 = 270 мм (см. черт. 30).

По формуле (81) определим длину зоны анкеровки l_an , принимая w _an = 0,5 и Dl _an = 8:

мм.

Поскольку l_x < l_an , расчетное сопротивление растянутой арматуры снижаем путем умножения его на коэффициент = 0,340, отсюда R_s = 365 · 0,340 = 124,1 МПа.

Поскольку к растянутым стержням в пределах длины l_x приварены четыре вертикальных и два горизонтальных поперечных стержня (см. черт. 30), увеличим усилие R_s A_s = 124,1 · 982 = 121,9 · 10³ H на величину N_w .

Принимая d_w = 6 мм, n_w = 6, j _w = 200 (см. табл. 22), получим

H.

Отсюда R_s A_s = 121,9 + 20,26 = 142,2 кН.

Поскольку эта величина не превышает значения R_s A_s , определенного без учета g _{s 5} и N_w , т. е. равного 365 · 982 = 358 · 10³ H, оставляем R_s A_s = 142,2 кН.

Высоту сжатой зоны определим по формуле (16):

Согласно п. 3.42 принимаем z_s = h ₀ – a’ = 360 – 35 = 325 мм.

По формуле (55) вычислим величину q_sw :

Н/мм.

Определим длину проекции невыгоднейшего наклонного сечения по формуле (83), принимав значение Q равным опорной реакции балки, т. е. Q = = 80 кН, а также F_i = 0 и A_s,inc =0:

мм.

Определим максимальную длину l_s приопорного участка, за которым выполняется условие (72), с умножением правой части на 0,8 и при с = c ₁ £ 0,8c_max = 2h ₀ , т. е. из решения уравнения

Предполагая, что l^s > 2h ₀ , принимаем максимальное значение c ₁ = 2h _0. Тогда при j _{b 4} = 1,5 получим

Поскольку l_s = 1760 мм > c = 821 мм, оставим с = 821 мм.

Момент внешних сил относительно оси, расположенной посредине высоты сжатой зоны наклонного сечения, в данном случае равен изгибающему моменту в нормальном сечении, проходящем через указанную ось, т. е. на расстоянии l ₁ + с = l_sup /3 + с = 280/3 + 821 = 914 мм от точки приложения опорной реакции:

Проверим прочность из условия (77) с учетом формулы (78):

т. е. прочность наклонных сечений на действие изгибающего момента обеспечена.

Поскольку балка не имеет отгибов и нагружена равномерно распределенной нагрузкой, прочность наклонного сечения можно также проверить по более простой формуле (84), принимая М ₀ = Ql ₁ = 80 · 10³ · 93 = 7,4 · 10⁶ Н · мм:

Пример 22. Дано: ригель многоэтажной рамы с эпюрами изгибающих моментов и поперечных сил от равномерно распределенной нагрузки q = 228 кН/м по черт. 31; бетон тяжелый класса В25; продольная и поперечная арматура класса А-III (R_s = 365 МПа; R_sw = 290 МПа); поперечное сечение приопорного участка — по черт. 31; хомуты диаметром 10 мм, шагом s = 150 мм (А_sw = 236 мм² ).

Требуется определить расстояние от левой опоры до места обрыва первого стержня верхней арматуры.

Черт. 31. К примеру расчета 22

Расчет. Определим предельный изгибающий момент, растягивающий опорную арматуру без учета обрываемого стержня, из условия (19), поскольку А_s = 1609 мм² < т. е. х < 0:

кН · м.

По эпюре моментов определим расстояние х от опоры до места теоретического обрыва первого стержня из уравнения

откуда

Поперечная сила в месте теоретического обрыва равна:

кН.

Определим величину q_sw :

Н/мм.

По формуле (87) вычислим длину w , на которую надо завести обрываемый стержень за точку теоретического обрыва:

мм.

Следовательно, расстояние от опоры до места обрыва стержня может быть принято равным x + w = 334 + 756 = 1090 мм.

• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11
• часть 12
• часть 13
• часть 14
• часть 15
• часть 16
• часть 17
• часть 18
• часть 19
• часть 20