RMNT.RU  /  Нормативные документы  /  СНиПы  /  Нормы проектирования

СНиП 2.05.03-84 (с изм. 1 1991), часть 27

П р и м е ч а н и я: 1. mf — коэффициент, учитывающий влияние сдвигов по контактам соединяемых элементов и принимаемый по табл. 3 в зависимости от числа поперечных рядов болтов n в соединении.

2. Параметр n определяется:

числом поперечных рядов болтов в прикреплении данного элемента к фасонке или стыковой накладке, когда этот элемент обрывается в данном узле (п. 3, г, д, е);

общим числом поперечных рядов болтов в прикреплении фасонки к непрерывному элементу (п. 3, в).

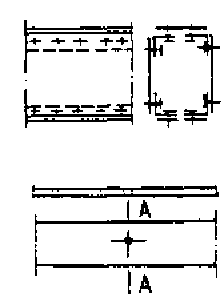
Черт. 1. Расположение проверяемого на выносливость расчетного сечения А—А по основному металлу в сечениях нетто
по соединительным болтам составных элементов,
а также у свободного отверстия

Черт. 2. Расположение проверяемого на выносливость расчетного сечения А—А по основному металлу в сечениях нетто
у отверстия с поставленным в него высокопрочным болтом,
затянутым на нормативное усилие

Черт. 3. Расположение проверяемого на выносливость расчетного сечения А—А по основному металлу в сечении брутто по первому ряду высокопрочных болтов в прикреплении фасонки
к нестыкуемым в данном узле поясам сплошных балок
и элементам решетчатых форм

Черт. 4. Расположение проверяемого на выносливость расчетного сечения А—А по основному металлу в сечении брутто
по первому ряду высокопрочных болтов в прикреплении к узлу или в стыке двухстенчатых элементов

Черт. 5. Расположение проверяемого на выносливость расчетного сечения А—А по основному металлу в сечении брутто по первому ряду высокопрочных болтов в прикреплении к узлу или в стыке двухстенчатых элементов с односторонними накладками

Черт. 6. Расположение проверяемого на выносливость расчетного сечения А—А по основному металлу в сечении брутто по первому ряду высокопрочных болтов в прикреплении к узлу или в стыке одностенчатых элементов с односторонними накладками

Таблица 2

Эффективные коэффициенты концентрации напряжений для расчета
на выносливость стальных канатов висячих, вантовых и предварительно напряженных стальных пролетных строений

Устройства, закрепляющие или отклоняющие канаты

Коэффициент

b s

1. Анкеры клинового типа

1,1

2. Анкеры с заливкой конца каната в конической или цилиндрической полости корпуса сплавом цветных металлов или эпоксидным компаундом

1,3

3. Анкеры со сплющиванием концов круглых проволок, защемлением их в анкерной плите и заполнением пустот эпоксидным компаундом с наполнителем из стальной дроби

1,1

4. Отклоняющие канат устройства, в том числе стяжки и сжимы, имеющие круговое очертание ложа, скругление радиусом 5 мм у торцов (в месте выхода каната) и укороченную на 40 мм (по сравнению с длиной ложа) прижимную накладку:


при непосредственном контакте каната со стальным ложем и поперечном давлении

1 МН/м (1 тс/см)

1,2

при контакте каната со стальным ложем через мягкую прокладку толщиной t ³ 1 мм и поперечном давлении

2 МН/м (2 тс/см)

1,2

5. Хомуты подвесок; стяжки и сжимы без отклонения каната при поперечном давлении:


q £ 1 МН/м (1 тс/см) и непосредственном контакте с канатом

1,1

q £ 2 МН/м (2 тс/см) и контакте с канатом через мягкую прокладку толщиной t ³ 1 мм

1,1

В табл. 2 обозначено:

N — усилие в канате, МН (тс);

r — радиус, м (см), кривой изгиба каната в отклоняющем устройстве

Таблица 3*

n

1-3

4-6

7-8

9-10

11-15

16 и более

mf

1,00

1,05

1,12

1,16

1,20

1,23


ПРИЛОЖЕНИЕ 18*

Обязательное

РАСЧЕТ ОРТОТРОПНОЙ ПЛИТЫ ПРОЕЗЖЕЙ ЧАСТИ
ПО ПРОЧНОСТИ И УСТОЙЧИВОСТИ

1. Метод расчета ортотропной плиты должен учитывать совместную работу листа настила, подкрепляющих его ребер и главных балок.

2. Ортотропную плиту допускается условно разделять на отдельные системы — продольные и поперечные ребра с соответствующими участками листа настила (см. чертеж).

Коробчатое пролетное строение

а — продольный разрез; б — план; в — поперечный разрез; г — ребро нижней плиты; 1, 2, 3, ... i — номер поперечного ребра верхней плиты

усилия в ортотропной плите при работе НА ИЗГИБ МЕЖДУ ГЛАВНЫМИ БАЛКАМИ

3. Изгибающие моменты в продольных ребрах ортотропной плиты следует определять по формуле

Мsi = М1 + М, (1)

M1  — изгибающий момент в отдельном продольном ребре полного сечения, включающего прилегающие участки листа настила общей шириной, равной расстоянию а между продольными ребрами (см. чертеж, в), рассматриваемом как неразрезная балка на жестких опорах; момент определяется от нагрузки, расположенной непосредственно над этим ребром;

М — изгибающий момент в опорном сечении продольного ребра при изгибе ортотропной плиты между главными балками, определяемый при загружении поверхности влияния нагрузкой, прикладываемой в узлах пересечения продольных и поперечных ребер.

Нагрузку, передаваемую с продольных ребер на узлы пересечения с поперечными ребрами, следует определять с помощью линии влияния опорной реакции неразрезной многопролетной балки на жестких опорах.

В пределах крайних третей ширины ортотропной плиты автопроезда и в ортотропной плите однопутных железнодорожных пролетных строений с ездой поверху следует принимать М = 0.

Ординаты поверхности влияния для вычисления изгибающего момента М в опорном сечении продольного ребра над «средним» поперечным ребром l (см. чертеж, а) следует определять по формуле

, (2)*

где M1i - принимаемые по табл. 1 (с умножением на l) ординаты линии влияния изгибающего момента в опорном сечении продольного ребра над «средним» поперечным ребром l при расположении нагрузки над поперечным ребром i;

l — пролет продольного ребра (см. чертеж, б);

L — пролет поперечного ребра (см. чертеж, в);

u — координата положения нагрузки от начала поперечного ребра.

Таблица 1

Номер попереч ного

Ординаты линии влияния при z

ребра i

0

0 ,1

0,

0,5

1,0

1

0

0,0507

0,0801

0,1305

0,1757

2

0

-0,0281

-0,0400

-0,0516

-0,0521

3

0

0,0025

-0,0016

-0,0166

-0,0348

4

0

0,0003

0,0016

0,0015

0,0046

5

0

-0,0001

0

0,0014

0,0025

6

0

0

0

0,0001

0,0012

В табл. 1 обозначено:

z - параметр, характеризующий изгибную жесткость ортотропной плиты и определяемый по формуле

,

где Isl - момент инерции полного сечения продольного ребра относительно горизонтальной оси (см. чертеж в);

a - расстояние между продольными ребрами;

Is - момент инерции полного поперечного ребра — с прилегающим участком настила шириной 0,2 L, но не более l — относительно горизонтальной оси х1 (см. чертеж, а).

П р и м е ч а н и е. В табл. 1 принята следующая нумерация поперечных ребер i : ребра 2—6 расположены на расстоянии l одно от другого в каждую сторону от «среднего» поперечного ребра 1 (см. чертеж, a).

4. В железнодорожных пролетных строениях лист настила ортотропной плиты проезжей части следует рассчитывать на изгиб, при этом прогиб листа настила не проверяется.

При устройстве пути на балласте наибольшие значения изгибающих моментов в листе настила над продольными ребрами следует определять по формулам:

в зоне под рельсом

My = -0,1 n a2 ; (3)

в зоне по оси пролетного строения

My = -0,08 n a2 , (4)

где n  — нагрузка на единицу длины, принимаемая по п. 2 обязательного приложения 5*.

РАСЧЕТ ЭЛЕМЕНТОВ ОРТОТРОПНОЙ ПЛИТЫ
ПО ПРОЧНОСТИ

5. Для проверки прочности элементов ортотропной плиты необходимо получить в результате расчетов в предположении упругих деформаций, стали в сечениях I , II, III и точках А, В, С, А1 , В1 , D1 , указанных на чертеже, нормальные напряжения в листе настила, продольных и поперечных ребрах, а также касательные напряжения в листе настила, от изгиба ортотропной плиты между главными балками s xp , s yp и t xyp и совместной работы ее с главными балками пролетного строения s xc , s y c и t xy c .

6. Проверку прочности растянутого при изгибе ортотропной плиты крайнего нижнего волокна продольного ребра следует выполнять в зоне отрицательных моментов неразрезных главных балок в сечении I—I посредине пролета l среднего продольного ребра (см. чертеж, а — точка A) по формулам:

ys xc + m1 c 1 s xp £ Ry m ; (5)

s xc + s xp £ m2 Ryn m , (6)

где Ry , Ryn  — расчетное и нормативное сопротивления металла продольного ребра;

m — коэффициент условий работы, принимаемый по табл. 60*;

m1 , m2  — коэффициенты условий работы; для автодорожных и городских мостов, а также для автодорожного проезда совмещенных мостов их следует принимать по табл. 2*; для железнодорожных и пешеходных мостов, а также для железнодорожного проезда совмещенных мостов m1 = 1 / ‘ ; при этом проверка по формуле (6) не выполняется;

c — коэффициент влияния собственных остаточных напряжений, принимаемый c 1 = 0,9  — для крайнего нижнего волокна продольного ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и c 1 = 1,1 — для продольного ребра в виде сварного тавра;

y , ‘ — коэффициенты, определяемые по пп. 4.28* и 4.26*.

Таблица 2*


s xc / s xp

Значения коэффициентов m1 и m2
для полосовых ребер


m1

m2

0

0,55

1,40

0,25

0,40

1,50

0,45

0,25

1,60

0,65

0,13

1,60

П р и м е ч а н и е. Коэффициенты m1 и m2 для промежуточных значений s xc / s xp следует определять линейной интерполяцией.

7. Проверку прочности сжатого при местном изгибе ортотропной плиты крайнего нижнего волокна продольного ребра следует выполнять в зоне положительных моментов неразрезных главных балок в опорном сечении II—III среднего продольного ребра (см. чертеж а — точка В) по формуле

s xp

ys xc + c 2 ¾ £ Ry m , (7)

‘

где y , ‘ — коэффициенты, определяемые по пп. 4.28* и 4.26*;

c 2 - коэффициент влияния собственных остаточных напряжений, принимаемый c 2 = 1,1 — для крайнего нижнего волокна ребра, выполненного из полосы, прокатного уголка или прокатного тавра, и c 2 = 0,9 — для ребра в виде сварного тавра;

m - коэффициент условий работы, принимаемый по табл. 60*.

8. Проверку прочности крайнего нижнего волокна поперечной балки следует выполнять в сечении III—III посредине ее пролета (см. чертеж в — точка С) по формуле

s yp

¾ £ Ry m , (8)

‘

где ‘ — коэффициент, определяемый по формулам (143) и (144);

m — коэффициент условий работы, принимаемый по табл. 60*.

9. Расчет по прочности листа настила следует выполнять в точках А1 , В1 , D1 (см. чертеж б) по формулам:

; (9)

t xy £ Rs m , (10)

где s x = s xc + m4 s xp ; s y = s yc + m4 s yp ;

t xy = t xyc + t xyp ;

m - коэффициент условий работы, принимаемый по табл. 60*;

m3  — коэффициент, равный 1,15 при s y = 0 или 1,10 при s y ¹ 0;

m4  — коэффициент условий работы, принимаемый равным 1,05 — при проверке прочности листа настила в точке A1 ортотропной плиты автодорожных и городских мостов и 1,0  — во всех остальных случаях.

При выполнении данной проверки допускается принимать в качестве расчетных загружения, при которых достигает максимального значения одно из действующих в данной точке ортотропной плиты напряжений s x , s y или t xy .

РАСЧЕТ ЭЛЕМЕНТОВ ОРТОТРОПНОЙ ПЛИТЫ
ПО УСТОЙЧИВОСТИ

10. Местная устойчивость листа настила между продольными ребрами, продольных полосовых ребер, свесов поясов тавровых продольных и поперечных ребер должна быть обеспечена согласно пп. 4.45* и 4.47, а стенки тавровых ребер — согласно обязательному приложению 16*. При этом следует выбирать наиболее невыгодную комбинацию напряжений от изгиба ортотропной плиты между главными балками и совместной ее работы с главными балками пролетного строения.

11. Общая устойчивость листа настила, подкрепленного продольными ребрами, должна быть обеспечена поперечными ребрами.

Момент инерции поперечных ребер Js (см. п. 3) сжатой (сжато-изогнутой) ортотропной плиты следует определять по формуле
, (11)*

где a — коэффициент, определяемый по табл. 2, а*;

y — коэффициент, принимаемый равным: 0,055 при k = 1; 0,15 при k = 2; 0,20 при k ³ 3;

k — число продольных ребер рассчитываемой ортотропной плиты;

L — расстояние между стенками главных балок или центрами узлов геометрически неизменяемых поперечных связей;

l — расстояние между поперечными ребрами;

Jsl  — момент инерции полного сечения продольного ребра (см. п. 3);

s xc  — действующие напряжения в листе настила от совместной работы ортотропной плиты с главными балками пролетного строения, вычисленные в предположении упругих деформаций стали;

s x,cr,ef  — напряжение, вычисленное по табл. 68* по значению s x,cr = s xc .

Таблица 2а*

w

0

0,1

0,2

0,3

0,4

0,5

a

0

0,016

0,053

0,115

0,205

0,320

Окончание таблицы 2а*

w

0,6

0,7

0,8

0,9

0,95

1

a

0,462

0,646

0,872

1,192

1,470

2,025

Допускается также определять s x,cr,ef по следующей формуле

s x,cr,ef = .

П р и м е ч а н и е. Коэффициент w определяется по формуле , где j 0 следует находить по табл. 3* п. 12 при lef = l .

Для сжатой ортотропной плиты, не воспринимающей местной нагрузки, в формуле (11)* коэффициент a следует принимать равным 2,025, что обеспечивает равенство расчетной длины lef продольных ребер расстоянию между поперечными ребрами l.

12*. Расчет по общей устойчивости ортотропной плиты в целом (сжатой и сжато-изогнутой) при обеспечении условия (11)* следует выполнять по формуле

s xc £ j 0 Ry m , (12)*

где s xc  — см. п. 11*;

j 0  — коэффициент продольного изгиба, принимаемый по табл. 3* в зависимости от гибкости l 0 ;

m — коэффициент условий работы, принимаемый по табл. 60* п. 4.19*.

Таблица 3*

Коэффициент j 0 для стали марок

Гибкость
l 0 , l 1


16Д


15ХСНД

10ХСНД ,
390-14Г2АФД ,
390-15Г2АФДпс

0

1,00

1,00

1,00

41

1,00

1,00

1,00

44

1,00

1,00

0,96

50

1,00

0,92

0,88

53

1,00

0,87

0,83

60

0,95

0,76

0,72

70

0,83

0,64

0,59

80

0,73

0,56

0,49

90

0,64

0,50

0,43

100

0,59

0,44

0,38

110

0,53

0,39

0,33

120

0,47

0,34

0,28

130

0,41

0,30

0,25

140

0,36

0,26

0,22

150

0,32

0,23

0,20

160

0,29

0,21

0,17

170

0,26

0,19

0,16

180

0,23

0,17

0,14

190

0,21

0,15

0,13

200

0,20

0,14

0,11

Гибкость следует определять по формуле

, (13)*

где lef - расчетная (свободная) длина продольных ребер, определяемая из выражения lef = l. Коэффициент w находят из табл. 2а* по значению

;

Js , Jsl и l - см. п. 3;

a - расстояние между продольными ребрами;

lh - толщина листа настила;

x - коэффициент, принимаемый равным 1,0 —для ортотропной плиты нижнего пояса и по табл. 4* — для плиты верхнего пояса коробчатых главных балок;

A - площадь полного сечения продольного ребра;

- (здесь Jt  — момент инерции полного сечения продольного ребра при чистом кручении).

Таблица 4*

f / i

Коэффициент x

0

1,00

0,01

0,75

0,05

0,70

0,10

0,66

f  — прогиб продольного ребра между поперечными ребрами;

i — радиус инерции полного сечения продольного ребра.

Сжато-изогнутую ортотропную плиту железнодорожных мостов на общую устойчивость следует проверять по формуле (167), принимая гибкость по формуле (13)* при x = 1,0.

13. Тавровые продольные ребра (см. чертежи, в, г) сжатой ортотропной плиты нижнего пояса коробчатых главных балок при изгибно-крутильной форме потери устойчивости следует рассчитывать по формуле (12)*, принимая коэффициент продольного изгиба j 0 в зависимости от гибкости l 1 .

Гибкость l 1 следует определять по формуле

, (14)

где Ip = Iy + Iz + A (hw - e)2 ;

l — см. п. 3;

hw  — высота стенки ребра толщиной tw (см. чертеж, г);

е — расстояние от центра тяжести полки шириной bf , толщиной tf до центра тяжести таврового продольного ребра (см. чертеж, г);

Iy , Iz  — соответственно момент инерции сечения таврового продольного ребра относительно горизонтальной оси у и вертикальной оси z;

;

;

A = bf tf + hw tw .

Для обеспечения местной устойчивости элементов таврового сечения продольного ребра толщина полки и стенки должна удовлетворять требованиям п. 4.45*:

при bf > 0,3 hw продольное ребро полного сечения следует считать двутавром, при bf = 0  — тавром;

при 0 < bf £ 0,3 hw требования к толщине стенки определяются по линейной интерполяции между нормами для двутавра и тавра (bf = 0).


ПРИЛОЖЕНИЕ 19

Обязательное

УЧЕТ ПОЛЗУЧЕСТИ, ВИБРОПОЛЗУЧЕСТИ БЕТОНА
И ОБЖАТИЯ ПОПЕРЕЧНЫХ ШВОВ
В СТАЛЕЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЯХ

1. При учете ползучести бетона в статически определимых конструкциях необходимо определить уравновешенные в пределах поперечного сечения (далее — внутренние) напряжения и соответствующие деформации.

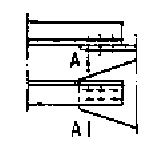
Эпюры относительных деформаций и внутренних напряжений
от ползучести бетона

Для конструкции, состоящей из стальной балки со сплошной стенкой и объединенной с ней в уровне проезда железобетонной плиты (см. чертеж), внутренние напряжения от ползучести бетона в общем случае надлежит определять по следующим формулам:

на уровне центра тяжести бетонной части сечения (растяжение)

s b,kr = -a s bl ; (1)

в крайней фибре нижнего пояса стальной балки (растяжение или сжатие)

; (2)

в крайней фибре верхнего пояса стальной балки (сжатие)

; (3)

в стержнях крайнего ряда ненапрягаемой арматуры плиты при Еr = Ers = Est (сжатие)

; (4)

потери предварительного напряжения напрягаемой арматуры (сжатие)

; (5)

в крайней фибре бетона (растяжение)

. (6)

Относительные деформации от ползучести бетона в уровне центра тяжести его сечения (см. чертеж) надлежит вычислять по следующим формулам:

относительные деформации, отвечающие напряжениям в стальной части сечения,

; (7)

относительные деформации, отвечающие напряжениям в бетонной части сечения,

. (8)

В формулах (1) — (8):

a , b , n — параметры, связанные с податливостью бетонной и стальной частей сечения и определяемые из выражений:

;

b = an ;

;

j kr = g f Eb cn - предельная характеристика ползучести бетона;

g f - принимается по табл. 8.

cn - нормативная деформация ползучести бетона, определяемая по п. 3.15 и обязательному приложению 11* , при уточнении с учетом указаний обязательного приложения 13*;

s bl , s bf,l - начальное напряжение сжатия соответственно на уровне центра тяжести сечения и в крайней фибре бетона от постоянных нагрузок и воздействий;

s sbf,kr - условное напряжение в уровне крайней фибры бетона, определяемое из выражения

;

Ast , Ist , Ws1,st , Ws2,st , Wrf,st - соответственно площадь, момент инерции, моменты сопротивления нижнего и верхнего поясов балки и крайнего ряда арматуры брутто стальной части сечения, включая арматуру;

- коэффициент приведения по п. 5.16.

Остальные обозначения соответствуют пп. 5.5, 5.19* и чертежу.

2. Ползучесть бетона допускается учитывать введением в расчет условного модуля упругости бетона Eef,kr , если в статически определимой конструкции все постоянные нагрузки, вызывающие напряжение в бетоне, прикладываются в одной стадии и при одной и той же схеме работы. Модуль Еef,kr следует определять по формуле

, (9)

где n , j kr - см. п. 1.

Внутренние напряжения от ползучести бетона для i -й фибры сечения следует вычислять по формуле

s i,kr = s i,ef - s i , (10)

где s i,ef , s i - напряжения от постоянных нагрузок, полученные при модуле упругости бетона соответственно Еef,kr и Eb .

3. При учете ползучести бетона в статически неопределимых конструкциях необходимо определить внутренние напряжения и внешние силовые факторы (опорные реакции, изгибающие моменты и пр.), а также соответствующие деформации.

Внутренние напряжения и внешние силовые факторы допускается вычислять методом последовательных приближений, принимая усилия s b,kr Ab в центре тяжести бетонной части сечения за нагрузки (здесь s b,kr и Аb принимаются по п. 1).

При этом, выполняя расчет методом сил, бетонную часть сечения надлежит учитывать следующим образом: с модулем Еef,kr (см. п. 2) — при определении основных и побочных перемещений; с модулем Еb  —при определении напряжений в центре тяжести бетона от внешних силовых факторов, вызванных ползучестью. Выраженные через j kr значения предельной характеристики ползучести, используемые для определения s b,kr и Еef,kr при последовательных приближениях, приведены в таблице.


Номер

Значение предельной характеристики ползучести бетона j kr при вычислении

приближения

напряжений от ползучести бетона на уровне центра тяжести
бетонной части сечения s b,kr

основных и побочных перемещений

1

j kr

0,5 j kr

2

0,5 j kr

0,38 j kr

3

0,38 j kr

0,32 j kr

4. Прогибы конструкции от ползучести бетона следует определять, рассматривая стальную часть сечения под действием сил s kr Ab , приложенных в уровне центра тяжести сечения бетона. Для статически определимых конструкций имеет место равенство s kr = s b,kr ; для статически неопределимых систем s kr равно сумме внутренних напряжений и напряжений от внешних силовых факторов, вызванных ползучестью.

5. Деформации обжатия замоноличенных бетоном поперечных швов сборной железобетонной плиты необходимо учитывать в расчетах, если продольная арматура плиты не состыкована в швах и при этом плита не имеет предварительного напряжения в продольном направлении.

Деформации обжатия поперечных швов следует учитывать введением в выражения для a , b , Еef,kr (см. пп. 1 и 2) обобщенной характеристики ползучести бетона и обжатия поперечных швов j kr,d , определяемой по формуле

, (11)

где L — длина сжатой постоянными нагрузками и воздействиями железобетонной плиты;

SD d  — суммарная деформация обжатия поперечных швов, расположенных на длине L;

j kr  — принимается по п. 1;

Еb , Rb  — принимаются по пп. 3.24* и 3.32*.

При отсутствии опытных данных величину D d , см, допускается вычислять по формуле

D d = 0,005 + 0,00035 bd , (12)

где bd  — ширина шва (зазор между торцами сборных плит).

6. Учет виброползучести бетона следует выполнять введением в расчет условного модуля упругости бетона Еn kr , вычисляемого по п. 2 с заменой j kr на jn kr , определяемой по формуле

, (13)

где  — характеристика цикла начальных напряжений в бетоне, определенных без учета виброползучести и ползучести;

j kr , cn  — принимаются по п. 1.

ПРИЛОЖЕНИЕ 20

Обязательное

ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ
В СТАЛЕЖЕЛЕЗОБЕТОННЫХ БАЛКАХ
ОТ УСАДКИ БЕТОНА И ТЕМПЕРАТУРНЫХ ВОЗДЕЙСТВИЙ

1. Напряжения в стали и бетоне для статически определимой конструкции, состоящей из стальной балки со сплошной стенкой и объединенной с ней в уровне проезда железобетонной плиты, надлежит определять по формулам:

а) от усадки бетона

, (1)

где

Astb,shr , Istb,shr  — приведенные к стали площадь и момент инерции брутто поперечного сечения сталежелезобетонной балки при модуле упругости бетона Eef,shr , определяемом по п. 5.9;

Аst  — площадь стальной части сечения, включая арматуру железобетонной плиты;

Sshr = Ast Zst,stb ;

Zst,stb  — расстояние от центра тяжести Аstb,shr до центра тяжести Ast ;

Z — расстояние от центра тяжести Аstb,shr до фибры, где определяется s shr (положительное направление оси Z принято вниз);

n shr = 0, n shr = 1 — при определении напряжений соответственно в бетоне и в стали;

Е — следует принимать равным при определении напряжений:

в бетоне — Еef,shr ;

в стальной балке — Еst ;

в ненапрягаемой арматуре — Еrs ;

в напрягаемой арматуре — Еrp ;

e shr  — предельная относительная деформация усадки бетона, принимаемая по п. 5.9;

б) от температурных воздействий

, (2)

где a = 1× 10-5 град-1 — коэффициент линейного расширения стали и бетона;

tmax = g f tn,max ;

g f  — принимается по табл. 17*;

tn,max  — принимается по п. 5.10;

Е — равно Еb , Еst , Еrs , Еrp при определении напряжений соответственно в бетоне, стальной балке, ненапрягаемой и напрягаемой арматуре;

Аstb,t , Istb,t  — приведенные к стали площадь и момент инерции брутто поперечного сечения сталежелезобетонной балки;

Z — расстояние от центра тяжести Аstb,t до фибры, где определяется s t .

В случаях повышения или понижения температуры стальной части конструкции в формуле (2) следует принимать:

At = 0,8 Awt + 0,3 Asl,t ; (3)

St = (0,4 hw - 0,8 Zbl,stb ) Awt + 0,3 Asl,t Zsl,stb ; (4)

n = n ti ,

где Awt  — площадь стальных вертикальных элементов (стенки, вертикальных полок поясных уголков, ламелей);

Аsl,t  — площадь стальных горизонтальных элементов нижнего пояса.

В случае повышения температуры железобетонной плиты в формуле (2) следует принимать:

; (5)

; (6)

n = n ti ¢ ,

где bsl , tsl , см, принимаются по п. 5.15.

Величины n ti и n ti ¢ , относящиеся к i -й точке сечения, в которой определяются напряжения, следует принимать по п. 5.10.

Остальные обозначения, принятые в формулах (3)—(6), соответствуют п. 5.5 и черт. 14.

2. При расчете статически неопределимых систем на температурные воздействия и усадку бетона геометрические характеристики сечения следует принимать по п.1.

ПРИЛОЖЕНИЕ 21

Обязательное

РАСПРЕДЕЛЕНИЕ СДВИГАЮЩИХ УСИЛИЙ ПО ШВУ
ОБЪЕДИНЕНИЯ ЖЕЛЕЗОБЕТОННОЙ ПЛИТЫ И СТАЛЬНОЙ КОНСТРУКЦИИ В СЛОЖНЫХ СЛУЧАЯХ ВОЗДЕЙСТВИЙ

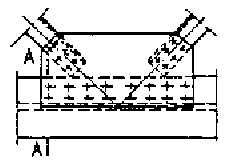
1. Распределение концевого сдвигающего усилия SeN следует принимать по несимметричной треугольной эпюре с длиной основания ae (см. чертеж).

Условные обозначения:

____________ максимальные значения;

__ __ __ __ __ минимальные «

Эпюры погонных сдвигающих сил между железобетонной
и стальной частями

I , II, III, IV — расчетная длина участков ai

При этом:

; , (1)

где SlN ¢ , SlN  — интенсивность погонных сдвигающих сил в соответствии с чертежом;

SeN , ae  — принимаются по пп. 5.28 и 5.29.

2. При распределении околоопорного сдвигающего усилия от поперечных сил SpQ следует принимать, что интенсивность соответствующих погонных сдвигающих сил изменяется в обе стороны по прямолинейной эпюре от середины длины околоопорного участка (см. чертеж); при этом ордината в середине околоопорного участка равна:

. (2)

3. Распределение местных сосредоточенных сдвигающих усилий (от заанкеривания высокопрочной арматуры, примыкания ванты или раскоса и т.д.) ScN в удаленных от конца плиты зонах следует принимать по симметричной треугольной эпюре с длиной основания 2ae (см. чертеж).

4. При определении сдвигающих усилий длины расчетных участков следует принимать (см. чертеж): I = 0,18 (H + bsl ), II = 0,36 (H + bsl ) — для концевых участков и в местах приложения сосредоточенных сил, а также в местах, примыкающих к указанному участку; III £ 0,8 (H + bsl ); IV £ 1,6 (Н + bsl )  — на остальной длине пролетного строения соответственно в крайней и средней четвертях пролета.

ПРИЛОЖЕНИЕ 22

Обязательное

РАСЧЕТЫ ПО ПРОЧНОСТИ ОБЪЕДИНЕНИЯ
ЖЕЛЕЗОБЕТОНА И СТАЛИ
ГИБКИМИ УПОРАМИ И АНКЕРАМИ

1. Сдвигающее усилие Sh , приходящееся на один гибкий упор, должно отвечать следующим условиям прочности:

для гибких упоров в виде прокатных швеллеров,

двутавров, уголков без подкрепляющих ребер

; (1)

для гибких упоров в виде круглых стержней при 2,5 < д/d £ 4,2

; (2)

для гибких упоров в виде круглых стержней при l /d > 4,2

. (3)

Для гибких упоров в виде круглых стержней должно быть, кроме того, выполнено условие

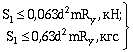. (4)

В формулах (1) — (4):

tfr  — сумма радиуса закругления и наибольшей толщины полки прокатного профиля, см;

tw  — толщина стенки прокатного профиля, см;

l — длина круглого стержня гибкого упора, см;

d — диаметр стержня гибкого упора или анкера, см;

bdr  — ширина площади смятия бетона упором, см;

Rb , Ry , m — принимаются согласно п. 5.19*.

2. Сдвигающее усилие, приходящееся на один наклонный анкер из арматурной стали круглого сечения (гладкого или периодического профиля) или на одну ветвь петлевого анкера, должно отвечать следующим условиям:

; (5)

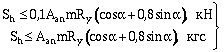, (6)

где Aan  — площадь поперечного сечения стержня анкера или ветви анкера, см2 ;

a — угол наклона анкера к поверхности стальной конструкции.

Для анкеров, разведенных в плане, в формулы (5) и (6) вместо cos a следует подставлять произведение cos a cos b , где b  — угол между горизонтальной проекцией анкера и направлением действия сдвигающей силы.

Сдвигающее усилие, воспринимаемое сжатыми наклонными анкерами, не должно превышать 25 % полного сдвигающего усилия, действующего на рассчитываемом участке.

3. При объединении железобетонной части со стальной с помощью наклонных анкеров из полосовой стали толщиной tan от 8 до 20 мм и шириной от 20 до 80 мм сдвигающее усилие Sh , приходящееся на один анкер или одну ветвь петлевого анкера, следует проверять по формуле (5), заменяя d2 выражением ( где tan - в см), и по формуле (6).

↑
Закрыть

Строительный каталог