• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11

, (100)

где М₀ - момент в сечении по грани опоры;

Q - поперечная сила в опорном сечении.

Для консолей, нагруженных сосредоточенными силами, невыгоднейшее наклонное сечение начинается от мест приложения сосредоточенных сил вблизи свободного конца и имеет длину проекции с для консолей с постоянной высотой сечения, равную:

, (101)

но не более расстояния от начала наклонного сечения до опоры. Здесь Q₁ - поперечная сила в начале наклонного сечения.

Для консолей, нагруженных только равномерно распределенной нагрузкой q, невыгоднейшее наклонное сечение заканчивается в опорном сечении и имеет длину проекции с, равную:

. (102)

При этом, если с < l - l_an или с < l - l_p , то в формуле (102) принимается соответственно R_s A_s = 0 или R_s A_sp = 0.

В формуле (102):

А_sp , А — площади сечения арматуры, доводимой до свободного конца;

l_p , l_an - длины зоны передачи напряжений и зоны анкеровки (см. пп. 2.26 и 5.32);

z_s - определяется для опорного сечения.

Для элементов с высотой сечения, увеличивающейся с увеличением изгибающего момента, при определении длины проекции невыгоднейшего сечения по формуле (99) или (101) числители этих формул уменьшаются на величину (R_s A_sp + R_s A_s )tg b при наклонной сжатой грани и на величину (R_s A_sp + R_s A_s )sin b при наклонной растянутой грани, где b - угол наклона грани к горизонтали.

3.34. Для обеспечения прочности наклонных сечений на действие изгибающего момента начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень полностью используется по моменту, не менее чем на h₀ /2, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб по расчету не требуется.

Примеры расчета

Пример 11. Дано: железобетонная плита перекрытия с размерами поперечного сечения по черт. 21; бетон тяжелый класса В25 (R_b = 13 МПа, R_bt = 0,95 МПа с учетом g _b2 = 0,9, Е_b = 27 × 10³ МПа); ребро плиты армировано плоским каркасом с поперечными стержнями из арматуры класса Вр-I , диаметром 5 мм (А_sw = 19,6 мм² , R_sw = 260 МПа, Е_s = 17 × 10⁴ МПа), шагом s = 150 мм; усилие обжатия от растянутой продольной арматуры Р = 130 кН; временная эквивалентная нагрузка n = 19 кН/м, нагрузка от собственного веса плиты и пола g = 4 кН/м; поперечная сила на опоре Q_max = 62 кН.

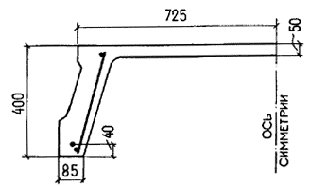
Черт. 21. К примеру расчета 11

Требуется проверить прочность по наклонной полосе ребра плиты между наклонными трещинами, а также прочность наклонных сечений по поперечной силе.

Р а с ч е т. h ₀ = 400 - 40 = 360 мм. Прочность бетона ребра плиты проверяем из условия (68).

Определим коэффициенты j _w1 и j _b1 :

= 0,00154 ;

;

отсюда j _w1 = 1 + 5 am _w = 1 + 5 × 6,3 × 0,00154 = 1,0485 < 1,3; j _b1 = 1 - b R_b = 1 - 0,01 × 13 = 0,87.

Тогда 0,3 j _w1 j _b1 R_b b h₀ = 0,3 × 1,0485 × 0,87 × 13 × 85 × 360 = 108 700 H > Q_max = 62 кН, т.е. прочность бетона ребра плиты обеспечена.

Прочность наклонного сечения по поперечной силе проверяем из условия (71) п. 3.22.

Определим величины М и q_sw :

j _b1 = 2 (см. табл. 29) .

Так как b ¢ _f - b = 725 - 85 = 640 мм > 3h ¢ _f = 3 • 50 = 150 мм, принимаем b'_f - b = 150 мм.

Тогда

.

Поскольку 1 + j _f + j _n = 1 + 0,184 + 0,447 > 1,5, принимаем 1 + j _f + j _n = 1,5 ;

M_b = j _b2 (1 + j _f + j _n ) R_bt b h₀ ² = 2 × 1,5 × 0,95 × 85 × 360² = 31,3 ´ 10⁶ H × мм = 31,3 кН × м;

34 Н/мм.

Проверим условие (78):

Q_{b, min} = j _b3 (1 + j _f + j _n ) R_bt b h₀ = 0,6 × 1,5 × 0,95 × 85 × 360 = 26 163 H (где j _b3 = 0,6, см. табл. 29);

36,3 Н/мм > q_sw = 34 Н/мм ,

т.е. условие (78) не выполняется;

следовательно, корректируем значение М_b :

M_b = 2h₀ ² q_sw j _b2 / j _b3 = 2 × 360² × 34= 29 ,38 × 10⁶ H × мм = 29,4 кН × м и принимаем с₀ = 2h ₀ = 2 × 360 = 720 мм.

Определим длину проекции невыгоднейшего наклонного сечения с:

q ₁ = g + n /2 = 4 + 19/2 = 13,5 кН/м (Н/мм).

Так как 0,56 q_sw = 0,56 × 34 = 19 Н/мм > q₁ = 13,5 Н/мм, значение с равно:

= 1 ,475 м.

Поскольку = 1,2 м < с= 1,475 м, принимаем с = 1,2 м и Q_b = Q_b,min = 26,16 кН.

Проверяем условие (71), принимая Q в конце наклонного сечения, т.е. Q = Q_max - q₁ c = 62 - 13,3 • 1,2 = 45,8 кН;

Q_b + q_sw c₀ = 26,46 + 34 • 0,72 = 50,6 кН > Q = 45,8 кН,

т.е. прочность наклонного сечения обеспечена.

При этом s = 150 мм <

= 366 мм

и, кроме того, s < h/2 = 400/2 = 200 мм, т.е. требования пп. 3.21 и 5.42 выполнены.

Пример 12. Дано: свободно опертый железобетонный ригель перекрытия пролетом l = 8,3 м нагружен равномерно распределенной нагрузкой: временной эквивалентной n = 114 кН/м и постоянной g = 46 кН/м; размеры поперечного сечения: b = 300 мм, h = 800 мм, h₀ = 700 мм; бетон тяжелый класса В30 (R_b = 15,5 МПа, R_bt = 1,1 МПа с учетом g _b2 = 0,9); хомуты сварные из арматуры класса А-III (R_sw = 290 МПа); усилие предварительного обжатия Р = 1600 кН.

Требуется определить диаметр и шаг хомутов у опоры, а также выяснить, на каком расстоянии от опоры и как может быть увеличен их шаг.

Р а с ч е т. Наибольшая поперечная сила в опорном сечении равна:

= 664 кН ,

где q = n + g = 114 + 46 = 160 кН/м.

Определим требуемую интенсивность хомутов приопорного участка согласно п. 3.23б.

Поскольку j _n = 0,1 = 0,693 > 0,5,

то принимаем „ = 0,5.

Из формулы (73) при j _f = 0 и j _b2 = 2 (см. табл. 29) получаем:

M_b = j _b2 (1 + j _n ) R_bt b h₀ ² = 2 × 1,5 × 1,1 × 300 × 700 = 485•10 H × мм = 485 кН × м;

q₁ = g + n /2 = 46 + 114 / 2 = 103 кН/м (Н/мм);

Q_b1 = 2 = 447 кН.

Так как = 745 кН > Q_max = 664 кН,

интенсивность хомутов определяется по формуле

= 124 ,3 Н/мм.

При этом = 155 > q_sw = 124,3 Н/мм,

следовательно, принимаем q_sw = 155 Н/мм.

Согласно п. 5.42, шаг у опоры должен быть не более 1/3h = 800/3 = 267 мм и не более 500 мм, а в пролете - не более 3/4h = 600 мм и не более 500 мм. Максимально допустимый шаг у опоры, согласно формуле (67), равен:

= 548 мм.

Принимаем шаг хомутов у опоры s₁ = 250 мм, а в пролете - 2s₁ = 500мм.

Отсюда А_sw = q_sw s / R_sw = 155 • 250/290 = 134 мм² .

Принимаем в поперечном сечении два хомута диаметром 10 мм (A_sw = 157 мм² ).

Тогда = 182 Н/мм ;

q_sw2 = 0,5q_sw1 = 91 Н/мм.

Длину участка с наибольшей интенсивностью хомутов q_sw1 определяем согласно п. 3.24.

Так как q_sw1 - q_sw2 = 182 - 91 = 91 Н/мм < q₁ = 103 Н/мм, значение с равно:

6 ,36 м > = 2 ,33 м.

Принимаем с = 2,33 м.

По формуле (77) при q_sw = q_sw1 = 182 Н/м вычисляем c₀₁ :

= 1 ,632 м.

Тогда =

1,45 м < = 2,08 м.

Принимаем длину участка с шагом хомутов s = 250 мм не менее 2,08 м.

Пример 13. Дано: железобетонная балка покрытия, нагруженная сосредоточенными силами, как показано на черт. 22, а; размеры поперечного сечения — по черт. 22, б; бетон тяжелый класса В50 (R_bt = 1,4 МПа при g _b2 = 0,9); хомуты из арматуры класса A-III (R_sw = 285 МПа); усилие предварительного обжатия Р = 640 кН.

Черт. 22. К примеру расчета 13

Требуется определить диаметр и шаг хомутов, а также выяснить, на каком расстоянии и как может быть увеличен их шаг.

Р а с ч е т. Сначала определим, согласно п. 3.22, величину М_b :

j _b2 = 2 (см. табл. 29); h'_f = 150 + 100/2 = 200 мм (см. черт. 22,б);

b'_f - b = 280 - 80 = 200 мм < 3h ¢ _f ; h₀ = 890 - 90 = 800 мм;

0,469 < 0,5 ;

= 0,714 > 0,5 .

Принимаем j _n = 0,5.

Поскольку 1 + j _f + j _n > 1,5, принимаем 1 + j _f + j _n = 1,5, M_b = j _b2 (1 + j _f + j _n ) R_bt b h₀ ² = 2 × 1,5 × 1,4 × 80 × 800² = 215 × 10⁶ Н × мм = 215 кН × м.

Определим требуемую интенсивность хомутов согласно п. 3.23а, принимая длину проекции наклонного сечения с равной расстоянию от опоры до первого груза - с₁ = 1,3 м.

Поперечная сила на расстоянии c₁ от опоры равна Q₁ = 288,6 кН (см. черт. 22, a).

Из формулы (72) имеем

164,5 кН > Q_b,min = j _b3 (1 + j _f + j _n ) R_bt b h₀ =
= 0,6 × 1,5 × 1,4 × 80 × 800 = 80,64 кН.

Тогда x₁ = = 0,75.

Поскольку c₁ = 1, 3 м < 2h₀ = 2 × 0,8 = 1,6 м, принимаем c₀ = c₁ = 1,3 м;

x₀₁ = = 0,396 .

Так как x₀₁ = 0,396 < x₁ = 0,75 < = 1, значения q_sw(1) определяем по формуле (80):

q_sw(1) = = 94,8 кН/м.

Определим q_sw(2) при значении с, равном расстоянию от опоры до второго груза, с₂ = 2,8 м:

= 76,8 кН < Q_b,min = 80,64 кН.

Принимаем Q_{b 2} = 80,6 4 кН.

Соответствующая поперечная сила равна Q ₂ = 205,2 кН.

Поскольку c ₂ = 2,8 м > 2h₀ = 1,6 м, принимаем c₀ = 2h₀ = 1,6 м;

1;

= 1,75.

Следовательно, значение q_sw(2) определяем по формуле (80):

77,85 кН/м.

Принимаем максимальное значение q_sw = q_sw(1) = 94,8 кН•м.

Согласно п. 5.42, шаг s₁ у опоры должен быть не более 1/3h = 890/3 = 297 мм и не более 500 мм, а в пролете — не более 3/4h = 3/4 • 890 = 667 мм и не более 500 мм. Максимально допустимый шаг у опоры, согласно формуле (67), равен:

s_mах = j _b4 (1+j _n ) R_bt bh₀ ² / Q_max = 1,5× 1,5× 1,4× 80× 800² /294,6× 10³ = 547 мм.

Принимаем шаг хомутов у опоры s₁ = 150 мм, а в пролете — s₂ = 2s₁ = 300 мм.

Отсюда = 50 мм² .

Принимаем одноветвевые хомуты диаметром 8 мм (А_sw = 50,3 мм² ).

Длину участка с шагом s₁ определяем из условия обеспечения прочности согласно п. 3.24.

При этом = 95,6 Н/мм; q_sw2 = 0,5 q_sw1 = 47 ,8 Н/мм; q_sw1 - q_sw2 = q_sw2 = 47,8 Н/мм.

Зададим длину участка с шагом хомутов s₁ = 150 мм равной расстоянию от опоры до второго груза l₁ = 2,8 м и проверим условие (71) при значении с, равном расстоянию от опоры до третьего груза: с = 4,3 м >l₁ .

Значение c₀₁ определим по формуле (77) при q_sw = q_sw1 = 95,6 кН/м:

= 1,5 м < 2h₀ = 1,6 м .

Так как с ₀₁ = 1,5 м = с - l₁ = 4,3 - 2,8 = 1,5 м, выражение q_sw c₀ заменим выражением q_sw2 (c - l₁ ) = 47,6 × 1,5 = 71,4 кН.

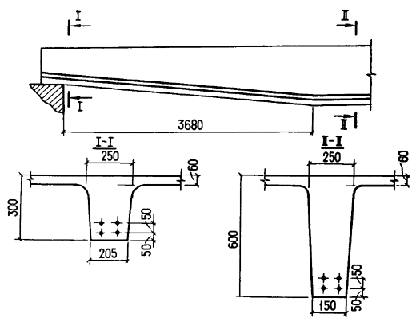
Q_b = М_b /с = 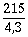= 50 кН < Q_b,min = 80,64 кН.

Принимаем Q_b = Q_b,min = 80,64 кН.

Соответствующая поперечная сила равна Q₃ = 121,8 кН (см. черт. 22, a).

Q_b + q_sw c₀ = 80,64 + 71,4 = 152,04 кН > Q₃ = 121,8 кН,

т. е. прочность наклонного сечения обеспечена.

Таким образом, длину участка с шагом хомутов s₁ = 150 мм принимаем равной l₁ = 2,8 м.

Пример 14. Дано: плита перекрытия с растянутой гранью, наклонной к горизонтали, с размерами по черт. 23; бетон тяжелый класса В40 (R_bt = 1,25 МПа с учетом g _b2 = 0,9); хомуты вертикальные класса А-III, диаметром 8 мм (R_sw = 285 МПа, A_sw = 50,3 мм² ) и шагом s = 100 мм; усилие предварительного обжатия Р = 980 кН; временная эквивалентная нагрузка n = 24,2 кН/м; постоянная нагрузка g = 7,8 кН/м; поперечная сила на опоре 186 кН.

Требуется проверить прочность наклонного сечения по поперечной силе.

Черт. 23. К примеру расчета 14

Р а с ч е т ведем согласно п. 3.27.

Из черт. 23 имеем h₀₃ = 300 — 75 = 225 мм. Размер b принимаем на уровне середины высоты опорного сечения:

= 233 мм.

Определим для опорного сечения величины j _fs , j _ns и M_bs по формулам (74), (75), (73):

b'_f - b = 3h ¢ _f = 3 • 60 = 180 мм;

= 0,154 ;

= 1,495 > 0,5 .

Принимаем 1 + j _fs + j _ns = 1,5 ; j _b2 = 2 (см. табл. 29);

M_bs = j _b2 (1 + j _fs + j _ns ) R_bt b h₀ ² = 2 × 1,5 × 1,25 × 233 × 225² = 44,2 • 10⁶ H × мм.

Определим величины q_sw и q_inc , принимая tg b = tg b ₁ = 0,0815:

= 143,3 Н/мм ;

q_inc = j _b2 (1 + j _fs + j _ns ) R_bt b tg² b = 2 × 1,5 × 1,25 × 233 × 0,0815² = 5,8 Н/мм;

q₁ = g + n /2 = 7,8 + 24,2/2 = 19,9 кН/м (Н/мм).

Проверим условие (87):

0,56 q_sw - 2,5 = 0,56 × 143,3 - 2,5 =
= 21,1 Н/мм > q₁ = 19,9 Н/мм.

Условие (87) выполняется, и, следовательно, невыгоднейшее значение с определяем по формуле (88) :

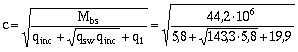= 901 мм.

Рабочая высота поперечного сечения на расстоянии с = 901 мм от опоры равна:

h ₀ = h _0s + ctgb = 225 + 901 × 0,0815 = 298мм,

а ширина ребра на уровне середины высоты h = 298+75 = 373 мм равна

= 226 мм.

Поскольку = 993 мм > с = 901 мм, оставляем с = 901 мм.

Определим соответствующее значение М_b , принимая 1+ j _fs + j _ns = 1,5:

М_b = 2 × 1,5 × 1,25 × 226 × 298² = 75,2 × 10⁶ H × мм.

Значение c₀ равно:

= 725 мм > 2h₀ = 2 × 298 = 596 мм.

Принимаем с ₀ = 596 мм.

Проверяем условие (71), принимая поперечную силу в конце наклонного сечения равной Q = Q_max - q₁ c = 186 — 19,9 × 0,901 = 168,1 кН:

= 83,5 × 10³ Н ;

Q_b + q_sw c₀ = 83,5 + 143,3 × 0,596 = 168,9 кН > Q = 168,1 кН,

т. е. прочность наклонного сечения обеспечена.

Пример 15. Дано: железобетонная двускатная балка покрытия с размерами по черт. 24 загружена сосредоточенными силами от плит покрытия и подвесных кранов, как показано на черт. 24,б; бетон тяжелый класса В40 (R_bt = 1,55 МПа при g _b2 = 1,1); хомуты двухветвевые из арматуры класса А-III, диаметром 10 мм (R_sw = 290 МПа, А_sw = 101 мм² ) и шагом s = 150 мм; усилие предварительного натяжения Р = 1220 кН.

Требуется проверить прочность наклонных сечений по поперечной силе.

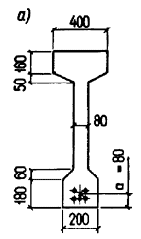
Черт. 24. К примеру расчета 15

Р а с ч е т ведем согласно п. 3.26. Проверим прочность наклонного сечения с длиной проекции, равной расстоянию от опоры до первого груза — с ₁ = 1,35 м.

Рабочая высота поперечного сечения в конце наклонного сечения равна:

h ₀ = 800 - 80 + 1350/12 = 832 мм.

Определим значение М_b согласно п. 3.22:

j _b2 = 2 (см. табл. 29); h ¢ _f = 160 + 50/2 = 185 мм;

b ¢ _f - b = 400 - 80 = 320 мм < 3h ¢ _f = 3 • 185 = 555 мм;

= 0,667 > 0,5 .

Принимаем j _f = 0,5;

= 1,18 > 0,5 .

Принимаем j _n = 0,5.

Поскольку 1 + j _f + j _n > 1,5, принимаем 1 + j _f + j _n = 1,5;

M_b = j _b2 ( 1 + j _f + j _n ) R_bt b h₀ ² = 2 × 1,5 × 1,55 × 80 × 832² = 257× 10⁶ H × мм = = 257 кН× м.

Значение q_sw равно:

= 303 Н/мм.

По формуле (77) определим длину проекции наклонной трещины:

= 921 мм = 0,921 м.

Так как с ₀₁ = 0,921 м < с₁ = 1,35 м и с ₀₁ < 2h₀ = 2 × 0,832 = 1,664 м, оставляем c₀₁ = 0,921 м.

Проверим условие (72), приняв Q в месте первого груза - Q₁ = 445 кН:

180 ,4 кН ;

Q_b + q_sw c₀₁ = 190,4 + 303 × 0,91 = 470 кН > Q₁ = 445 кН,

т.е. прочность этого наклонного сечения обеспечена.

Аналогично проверим прочность наклонного сечения с длиной проекции, равной расстоянию от опоры до второго груза  — с₂ = 2,85м:

h₀ = 720 + 2850 / 12 = 957 мм.

Поскольку = 3,19 м > c₂ = 2,85 м, оставляем c₂ = 2,85 м.

1 + j _fs + j _ns = 1,5 ;

М_b = 2 × 1,5 × 1,55 × 80 × 957² = 341 × 10⁶ Н × мм;

= 1060 мм < с₂ = 2,85 м ;

с ₀₂ < 2h₀ = 2 × 0,957 = 1,914 м.

Оставляем c₀₂ = 1060 мм;

H > Q₂ = 400 кН ,

т.е. прочность этого наклонного сечения также обеспечена.

Пример 16. Дано: многопустотная плита перекрытия пролетом l = 5,85 м с поперечным сечением по черт. 25; бетон тяжелый класса В25 (R_bt = 0,95 МПа с учетом g _b2 = 0,9 , E_b = 27 × 10³ МПа); усилие обжатия от каждого растянутого стержня Р = 69,2 кН; характеристики приведенного сечения шириной 0,2 м: площадь А_red = 24,7 × 10³ мм² ; момент инерции I_red = 183,3 × 10⁶ мм⁴ ; расстояние от центра тяжести до растянутой грани у₀ = 107 мм; временная эквивалентная нагрузка y = 12 кН/м² ; нагрузка от собственного веса плиты и пола g = 6 кН/м² .

Требуется выяснить, необходима ли в плите поперечная арматура.

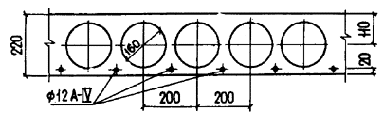
Черт. 25. К примеру расчета 16

Р а с ч е т. Проверим условия прочности согласно п. 3.30:

h ₀ = 220 - 20 = 200 мм.

Расчет ведем для ширины плиты, равной расстоянию между центрами круглых отверстий, т.е. b ¢ _f = 200 мм, b = 40 мм.

Тогда q = (6 + 12)0,2 = 3,6 кН/м = 3,6 Н/мм;

q₁ = (6 + 12/2)0,2 = 2,4 кН/м = 2,4 Н/мм.

Поперечная сила в опорном сечении = 10,52 кН.

Проверим условие (92):

2,5R_bt b h₀ = 2,5 • 0,95 • 40 • 200 = 19 000 H > Q_max = 10,52 кН,

т. е. условие (92) выполняется.

Проверим условие (93), принимая значение с равным М_b1 / Q_crc и длине участка l₁ без нормальных трещин. Для этого определим значение M_b1 и Q_crc , принимая

= 0,63 > 0,5 ,

т.е. j _n = 0,5 и j _b4 = 1,5 (см. табл. 29).

M_b1 = j _b4 (1 + j _n ) R_bt b h₀ ² = 1,5(1 + 0,5)0,95 × 40 × 200² = 3,42 × 10⁶ H × мм.

Статический момент части сечения, расположенной выше оси, проходящей через центр тяжести, S_red равен:

936 × 10³ мм³ ,

где D = 160 мм (см. черт. 25).

Из графика на черт. 18

при = 2,95

находим t = 1,99, т.е. t _xy,crc = t R_bt = 1,99 × 0,95 = 1,89 МПа .

Тогда = 14,8 × 10³ Н.

Поскольку Q_max = 10,52 кН < Q_crc = 14,8 кН, прочность наклонного сечения с длиной проекции с = M_b1 / Q_crc заведомо обеспечена.

Определим длину участка l₁ без нормальных трещин, т.е. расстояние от опоры до нормального сечения, в котором

Определим момент M_crc согласно п. 4.2, принимая в целях упрощения расчета W_pl = 1,5 W_red и j = 0,8:

1,72 × 10⁶ мм³ ;

W_pl = 1,5 × 1,72 × 10⁶ = 2,58 × 10⁶ мм³ ;

= 55,7 мм ;

е₀ = y₀ - a = 107 - 20 = 87 мм ;

M_crc = P(e₀ + r) + R_bt W_pl = 69,2 • 10³ (87 + 55,7) + 0,95 × 2580 × 10³ =
= 12,33 × 10³ H × мм.

Из вышеприведенного квадратного уравнения находим с = l₁ :

= 1,622 м > 2,5 h₀ = 2,5 × 0,2 = 0,5м.

Следовательно,

Q_b1 = Q_b,min = j _b3 (1 + j _n ) R_bt b h₀ = 0,6 × 1,5 × 0,95 × 40 × 200 = 6840 H.

Поперечная сила в конце наклонного сечения равна:

Q = Q_max - q₁ c = 20,32 - 2,4 × 1,622 = 6,41 кН < Q_b1 = 6,84 кН,

т.е. условие (93) выполнено. Следовательно, поперечную арматуру в плите можно не устанавливать.

Пример 17. Требуется по данным примера 11 проверить прочность наклонных сечений на действие изгибающего момента, принимая растянутую продольную арматуру ребра плиты в виде одного напрягаемого стержня класса A-V, диаметром 22 мм (R_s = 680 МПа, А_sp = 380 мм² ) и одного ненапрягаемого стержня класса Вр-I, диаметром 5 мм (R_s = 360 МПа, А_s = 19,6 мм² ); оба стержня постоянных анкеров не имеют; передаточная прочность бетона R_bp = 15 МПа; предварительное напряжение стержня с учетом потерь от релаксации и от технологических анкеров s _sp1 = 660 МПа (потери от температурного перепада, трения и деформации форм равны нулю); длина площадки опирания l_sup = 150 мм; характеристики приведенного сечения: площадь А_red = 68 800 мм² , момент инерции I_red = 1125 × 10⁶ мм⁴ , расстояние от центра тяжести до растянутой грани у₀ = 275 мм.

Р а с ч е т производим согласно пп. 3-31 - 3.33. Поскольку продольная арматура не имеет анкеров, расчетное сопротивление арматуры R_s определяем с учетом коэффициента условий работы g _b5 согласно поз. 3 табл. 23. Начало наклонного сечения принимаем у грани опоры. Следовательно, l_x = l_sup = 150 мм. Для напрягаемого стержня длину передачи напряжений l_р определяем по формуле (19). Из табл. 24 имеем w _p = 0,25, l _p = 10. Поскольку R_s = 680 МПа > s _sp1 = 660 МПа, принимаем s _tp = R_s = 680 МПа.

= 469 мм > 15d =
= 15 × 22 = 330 мм.

Оставляем l_p = 469 мм.

Отсюда для напрягаемого стержня = 0,32 и R_s = 680 g _s5 = 680 × 0,32 = 218 МПа.

Для ненапрягаемого стержня длину анкеровки определяем по формуле (301) п. 5.32. Поскольку стержень располагается в сжатом от действия опорной реакции бетоне, принимаем w _an = 0,5; Dl _an = 8;

102 мм < 200 мм.

Принимаем l_an = 200 мм. Тогда:

= 0,7 ;

R_s = 360 g _s5 = 360 × 0,7 = 252 МПа .

Высоту сжатой зоны х определяем как для прямоугольного сечения по формуле (26), принимая g _s6 = 1, b = b'_f = 725 мм, A'_sp = 0 и A ¢ _s = 0:

= 9,3 мм < h ¢ _f = 50 мм.

Тогда z = h₀ - 0,5x = 360 - 0,5 × 9,3 = 355,2 мм. Из примера 11 имеем q_sw = 34 Н/мм.

Определим длину проекции невыгоднейшего наклонного сечения по формуле (99), принимая F_i = 0, A_s,inc = 0, q = n + g == 19 + 4 = 23 Н/мм = 23 кН/м:

= 1088 мм.

Определим длину приопорного участка l₁ , на котором Q ³ Q_crc , т.е. из уравнения Q = Q_max - q₁ l₁ = Q_crc .

Вычисляем значение Qcrc согласно п. 3.30. Из графика на черт. 18 при

= 1,99

находим t = 1,73, т.e. t _xy,crc = R_bt t = 0,95 × 1,73 = 1,64 МПа. Статический момент S_red равен:

S_red = b (h - y₀ )² / 2 + (b'_f - b)h'_f (h - y₀ - h'_f /2) = 85(400 - 275)² /2 +

+ (725 - 85)50(400 - 275 - 50/2) = 38 640 × 10³ мм³ .

Тогда = 40,7 × 10³ H ;

= 1,58 мм.

Поскольку с = 1,088 м < l₁ = 1,58 м, значение с не корректируем.

Момент внешних сил относительно оси, проходящей через точку приложения равнодействующей усилий в сжатой зоне, в данном случае равен изгибающему моменту в нормальном сечении, проходящем через указанную ось, т.e. на расстоянии (l _у + с) от точки приложения опорной реакции, где l_у = l_sup / 3 = 50 мм — расстояние от этой точки до конца закладной детали (черт. 26):

Черт. 26. К примеру расчета 17

=
= 55,6 кН × м.

Проверяем прочность из условия (96), с учетом формулы (97):

(R_s A_sp + R_s A_s )z_s + 0,5 q_sw c² = (218 × 380 + 252 × 19,6) 355,2 + 0,5 × 34 × 1088² = 31,2 × 10⁶ +20,1 × 10⁶ = 51,3 × 10⁶ H × мм = 51,3 кН × м < М = 55,6 кН × м,

т.е. прочность наклонных сечений на действие изгибающего момента не обеспечена.

Добавляем на приопорном участке дополнительную сетку длиной l₁ = 300 мм с поперечными стержнями того же диаметра и шага, что и в основном плоском каркасе, и снова проверяем прочность сечения. Тогда, согласно п. 3.33, имеем:

q_sw2 = q_sw = 34 Н/мм; q_sw1 - q_sw2 = q_sw = 34 Н/мм ;

= 909 мм ;

l_y + с = 50 + 909 = 959 мм;

M = 62 × 0,959 = 48 ,9 кН × м .

Проверяем условие (96), принимая

S R_sw A_sw z_sw = 0,5 q_sw2 c² + (q_sw2 - q_sw1 )l₁ (c - l₁ /2) = 0,5 × 34 × 909² +
+ 34 × 300 (909 - 150) = 21,8 × 10⁶ H × мм = 21,8 кН × м;

(R_s A_sp + R_s A_s ) z_s + S R_sw A_sw z_sw = 31,2+21,8 = 53 кН × м > М = 48,9 кН × м,

т.е. прочность наклонного сечения обеспечена.

Внецентренно сжатые элементы

ОБЩИЕ ПОЛОЖЕНИЯ

3.35 (1.21). При расчете по прочности внецентренно сжатых железобетонных элементов должен приниматься во внимание случайный эксцентриситет е_а , обусловленный не учтенными в расчете факторами. Эксцентриситет е_а в любом случае принимается не менее:

1/600 всей длины элемента или расстояния между его сечениями, закрепленными от смещения;

1/30 высоты сечения элемента;

10 мм (для конструкций, образуемых из сборных элементов, при отсутствии других экспериментально обоснованных значений е_а ).

Для элементов статически неопределимых конструкций (в том числе для колонн каркасных зданий) значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения е₀ принимается равным эксцентриситету, полученному из статического расчета конструкций, но не менее е_а .

В элементах статически определимых конструкций (например, фахверковые стойки, стойки ЛЭП) эксцентриситет е₀ находится как сумма эксцентриситетов — определяемого из статического расчета конструкции и случайного.

3.36 (3.19, 3.3). При расчете внецентренно сжатых элементов необходимо учитывать влияние на их несущую способность прогибов в плоскости эксцентриситета продольного усилия (плоскости изгиба) и в нормальной к ней плоскости согласно указаниям п. 3.39. В случае расчета из плоскости изгиба значение е₀ принимается равным значению случайного эксцентриситета.

Расчет из плоскости изгиба можно не производить, если гибкость элемента l₀ /i (для прямоугольных сечений - l₀ /h) в плоскости изгиба превышает гибкость в плоскости, нормальной к плоскости изгиба.

При наличии расчетных эксцентриситетов в двух направлениях, превышающих случайные эксцентриситеты е_а , производится расчет на косое внецентренное сжатие.

3.37. Для наиболее часто встречающихся видов сжатых элементов (прямоугольного и двутаврового сечений с симметричной арматурой, сосредоточенной у наиболее сжатой и у растянутой граней, кольцевого сечения с арматурой, равномерно распределенной по окружности) расчет по прочности нормальных сечений при расположении продольной силы в плоскости симметрии производится согласно пп. 3.41—3.43. При этом граничное значение относительной высоты сжатой зоны x _R , коэффициент условий работы арматуры g _s6 и напряжение s _sc в напрягаемой арматуре, расположенной в сжатой зоне, определяются как для изгибаемых элементов согласно пп. 3.6 - 3.8.

Для других видов сечений, а также при косом внецентренном сжатии расчет нормальных сечений производится по формулам общего случая расчета нормальных сечений изгибаемых элементов согласно п. 3.18; при этом в правую часть уравнения (61) добавляется значение N, а за М в условии (60) принимается момент продольной силы N относительно оси, параллельной прямой, ограничивающей сжатую зону и проходящей через центр тяжести сечения растянутого стержня, наиболее удаленного от указанной прямой.

3.38. Расчет по прочности наклонных сечений внецентренно сжатых элементов производится аналогично расчету изгибаемых элементов в соответствии с указаниями пп. 3.19 - 3.34, учитывая влияние продольной силы N путем добавления ее к значению Р в формуле (75). При этом влияние продольных сил не учитывается, если они создают изгибающие моменты, одинаковые по знаку с моментами от действия поперечной нагрузки. Для внецентренно сжатых элементов статически неопределимых конструкций, при статическом расчете которых принимается, что продольная сила располагается в центре тяжести сечения, допускается всегда учитывать влияние продольных сил.

УЧЕТ ВЛИЯНИЯ ПРОГИБА ЭЛЕМЕНТА

3.39 (3.24, 3.6). При расчете внецентренно сжатых элементов следует учитывать влияние прогиба на их несущую способность, как правило, путем расчета конструкций по деформированной схеме, принимая во внимание неупругие деформации материалов и наличие трещин.

Допускается производить расчет конструкций по недеформированной схеме, учитывая при гибкости l₀ /i > 14 влияние прогиба элемента путем умножения эксцентриситета е₀ на коэффициент h , определяемый по формуле

, (103)

где N _сr  — условная критическая сила, принимаемая равной :

, (104)

где I, I_s  — моменты инерции соответственно бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения;

j _l  — коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии, равный:

, (105)

но не более 1 + b ,

здесь b  — коэффициент, принимаемый в зависимости от вида бетона по табл. 30;

M₁ , M_{1 l}  — моменты внешних сил относительно оси, проходящей через центр тяжести крайнего ряда арматуры, расположенного у растянутой (менее сжатой) грани, параллельной этой грани, соответственно от действия полной нагрузки и от действия постоянной и длительной нагрузок;

d _e  — коэффициент, принимаемый равным e₀ /h, но не менее

d _e,min = 0,5 - 0,01 - 0,01 R_b , (106)

здесь R_b  — в МПа, допускается принимать при g _b2 = 1,0;

l₀  — принимается по указаниям п. 3.40,

j _p  — коэффициент, учитывающий влияние предварительного напряжения арматуры на жесткость элемента; при равномерном обжатии сечения напрягаемой арматурой j _p определяется по формуле

, (107)

здесь s _bp  — определяется с учетом всех потерь при коэффициенте g _sp <1,0;

 — принимается не более 1,5;

R_b  — принимается без учета коэффициентов условий работы.

Для круглых и кольцевых сечений за величину h в формулах (106) и (107) принимается диаметр сечения D.

При гибкости l₀ /i £ 35 (для прямоугольных сечений - при l₀ /h £ 10) и при m < 0,015 допускается принимать

.

Таблица 30 (30)

Бетон	Коэффициент b в формуле (105)
1. Тяжелый	1,0
2. Мелкозернистый групп:
А	1,3
Б	1,5
В	1,0
3. Легкий
при искусственных крупных заполнителях и мелком заполнителе:
плотном	1,0
пористом	1,5
при естественных заполнителях	2,5

П р и м е ч а н и е. Группы мелкозернистого бетона приведены в п. 2.1.

Для элементов из мелкозернистого бетона группы Б в формулу (104) вместо значения 6,4 подставляется 5,6.

При N ³ N_cr следует увеличивать размеры сечения.

При расчетных эксцентриситетах в двух направлениях коэффициент h определяется отдельно для каждого направления и умножается на соответствующий эксцентриситет.

3.40. Для внецентренно сжатых элементов, имеющих несмещаемые опоры (например, фахверковые стойки), а также для элементов, не связанных с другими конструкциями (например, стойки ЛЭП), расчетные длины l₀ определяются из расчета на устойчивость.

Расчетные длины колонн одноэтажных и многоэтажных зданий принимаются согласно указаниям «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры».

РАСЧЕТ ЭЛЕМЕНТОВ СИММЕТРИЧНОГО СЕЧЕНИЯ
ПРИ РАСПОЛОЖЕНИИ ПРОДОЛЬНОЙ СИЛЫ
В ПЛОСКОСТИ СИММЕТРИИ

ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ
С СИММЕТРИЧНОЙ АРМАТУРОЙ

3.41. Расчет прямоугольных течений с симметричной арматурой (черт. 27), сосредоточенной у наиболее сжатой и у растянутой (менее сжатой) граней элемента, производится в зависимости от относительной высоты сжатой зоны следующим образом:

: (108)

Черт. 27. Схема усилий в прямоугольном сечении внецентренно сжатого железобетонного элемента

а) при x ₁ £ x _R (см. табл. 26 и 27 - из условия

Ne £ R_b bx (h₀ - 0,5 х) + s _sc A ¢ _sp (h₀ - a ¢ _p ) + R_sc A ¢ _s (h₀ - a ¢ _s ) , (109)

где . (110)

Коэффициент g _s6 определяется no формуле (27), принимая x ₁ по формуле (108) и ; допускается коэффициент g _s6 определять по формуле (23) п. 3.7, принимая x = x ₁ ;

б) при x ₁ > x _R — также из условия (109); при этом, если применяется арматура с условным пределом текучести (см. п. 2.16), высота сжатой зоны х определяется по формуле

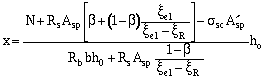, (111)

где x _el  — определяется по формуле

,

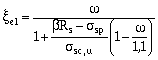здесь w , s _sc,u и s _sp  — см. п. 3.6;

b  — см. п. 3.18; при b = 0,8, т.е. при электротермическом и электротермомеханическом неавтоматизированных способах натяжения арматуры классов A-IV, A-V и A-VI, а также для прочих классов арматуры при любом способе натяжения значение можно определить по табл. 31 (для элементов из тяжелого бетона) или по табл. 32 (для элементов из легкого бетона или мелкозернистого бетона группы А).

Таблица 31

Коэффи циент условий	Класс растянутой	Обозначе-		Значения w , и x el для тяжелого бетона классов
работы бетона g b2	арматуры	ние		В15	В20	В25	В30	В35
1	2	3	4	5	6	7	8	9
0,9	Любой		Любое «	0,788 1761	0,766 1645	0,746 1553	0,726 1471	0,710 1409
	А-IV	x el	1 ,0	0,84	0,82	0,80	0,78	0,77
			0,8	0,79	0,77	0,75	0,73	0,71
			0,6	0,74	0,72	0,70	0,68	0,66
			0,4	0,71	0,68	0,66	0,64	0,62
	A-V		1,0	-	0,83	0,82	0,80	0,79
			0,8	-	0,77	0,75	0,73	0,71
			0,6	-	0,71	0,69	0,66	0,65
			0,4	-	0,66	0,63	0,61	0,60
	A-VI		1,0	-	0,85	0,83	0,82	0,80
			0,8	-	0,77	0,75	0,73	0,71
			0,6	-	0,70	0,68	0,65	0,64
			0,4	-	0,64	0,62	0,59	0,58
	К-7 ( Æ 12, Æ 15); В-II ( Æ 5, Æ 6); Вр-II ( Æ 4, Æ 5)		1,0 0,8 0,6 0,4	- - - -	0,88 0,77 0,68 0,60	0,87 0,75 0,65 0,58	0,85 0,73 0,63 0,56	0,84 0,71 0,61 0,54
1,0; 1,1	Любой		Любое «	0,775 1351	0,750 1254	0,722 1163	0,698 1093	0,698 1042
	A-IV	x el	1 ,0	0,84	0,82	0,79	0,77	0,75
			0,8	0,78	0,75	0,72	0,70	0,68
			0,6	0,72	0,69	0,66	0,64	0,62
			0,4	0,67	0,64	0,61	0,69	0,67
	A-V		1 ,0	-	0,84	0,82	0,80	0,78
			0,8	-	0,75	0,72	0,70	0,68
			0,6	-	0,68	0,65	0,62	0,60
			0,4	-	0,62	0,59	0,56	0,54
	A-VI		1,0	-	0,86	0,84	0,82	0,80
			0,8	-	0,75	0,72	0,70	0,68
			0,6	-	0,66	0,63	0,61	0,59
			0,4	-	0,60	0,56	0,54	0,52
	К-7 ( Æ 9, Æ 12, Æ 15); В-II ( Æ 5, Æ 6); Вр-II ( Æ 4, Æ 5)		1,0 0,8 0,6 0,4	- - - -	0,91 0,75 0,64 0,56	0,89 0,72 0,61 0,52	0,87 0,70 0,58 0,50	0,86 0,68 0,56 0,48

• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11