RMNT.RU  /  Нормативные документы  /  СанПиНы, руководящие документы  /  Пособия

Предварительно напряженные ЖБК (к СНиП 2.03.01-84), часть 6

Обозначения, принятые в табл. 27:

s sp  — см. табл. 26;

Ds sp  — см. п. 3.6;

.

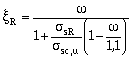П р и м е ч а н и я: 1. При подборе арматуры, когда неизвестно напряжение s sp , допускается значение определять при ( s sp + Ds sp ) / Rs = 0,6.

2. Приведенные значения вычислены без учета коэффициентов g bi по табл. 14.

3.7 (3.13). Если соблюдается условие x < x R , расчетное сопротивление арматуры Rs в оговоренных случаях умножается на коэффициент условий работы g s6 , определяемый по формуле

g s6 = h - ( h - 1) £ h , (23)

где h - коэффициент, принимаемый равным для арматуры классов:

A-IV............................................................ 1,20

A-V, В-II , Вр-II, К-7 и К-19 ...................... 1,15

A-VI ........................................................... 1,10

прочих ....................................................... 1,00

Если x < 0,5 x R , можно, не пользуясь формулой (23), принимать g s6 = h .

Коэффициент g s6 не следует учитывать для арматуры элементов:

рассчитываемых на действие многократно повторяющейся нагрузки;

армированных высокопрочной проволокой, расположенной вплотную (без зазоров);

эксплуатируемых в агрессивной среде;

в зоне передачи напряжений (см. п. 2.26).

При наличии сварных стыков в зоне элементов с изгибающими моментами, превышающими 0,9Мmax (где Мmax - максимальный расчетный момент), значение g s6 для арматуры классов A-IV и A-V принимается не более 1,1, а для арматуры класса A-VI - не более 1,05.

3.8 (3.14). Напрягаемая арматура, расположенная в сжатой от действия внешних сил зоне и имеющая сцепление с бетоном, вводится в расчет с напряжением s sc , равным ( s sc,u - s 'sp ) , но не более Rsc , где s 'sp определяется при коэффициенте g sp > 1,0, s sc,u  — см. п. 3.6.

ПРЯМОУГОЛЬНЫЕ СЕЧЕНИЯ

3.9 (3.15). Расчет прямоугольных сечений с арматурой, сосредоточенной у растянутой и сжатой граней элемента (черт. 5), производится в зависимости от относительной высоты сжатой зоны следующим образом:

; (24)

а) при x 1 £ x R  — из условия

М £ Rb bx (h0 - 0,5x) + Rsc A ¢ s (h0 - a ¢ s ) + s sc A ¢ sp (h0 - a ¢ p ) , (25)

где . (26)

Здесь коэффициент g s6 определяется по формуле

, (27)

где ;

h - см. п. 3.7.

Черт. 5. Поперечное прямоугольное сечение изгибаемого
железобетонного элемента

Допускается коэффициент g s6 определять по формуле (23) п. 3.7, принимая x = x 1 по формуле (24);

б) при x > x R  — из условия

M £ Rb bh0 2 + Rsc A ¢ s (h0 - a ¢ s ) + s sc A ¢ sp (h0 - a ¢ p ) . (28)

В условии (28) значения a R и a m вычисляются по формулам:

a R = x R (1 - 0,5 x R ) ; a m = x 1 (1 - 0,5 x 1 )

или находятся по табл. 28; x R - см. п. 3.6.

При напрягаемой арматуре растянутой зоны классов А-IIIв и А-III значение ( a R + a m ) / 2 в условии (28) заменяется на a R .

Если в растянутой зоне элемента имеется в большом количестве ненапрягаемая арматура с физическим пределом текучести (при Rs As > 0,2Rs Asp  — см. п. 2.16), то при напрягаемой арматуре с условным пределом текучести в условии (28) величина ( a R + a m ) / 2 заменяется на a R , а при напрягаемой арматуре с физическим пределом текучести значения x R и a R определяются по ненапрягаемой арматуре. В этих случаях, если x > x R , несущую способность сечения при необходимости можно несколько увеличить, произведя расчет по формулам общего случая согласно п. 3.18.

Если по формуле (26) х < 0, то прочность сечения проверяется из условия

M £ ( h Rs Asp + Rs As ) (h0 - a's ). (29)

3.10. В целях экономичного использования растянутой арматуры изгибаемые элементы рекомендуется проектировать так, чтобы выполнялось условие x £ x R .

3.11. Продольная арматура S при отсутствии напрягаемой арматуры в сжатой зоне подбирается следующим образом.

Вычисляется значение

. (30)

Если a m £ a R = x R (1 — x R / 2) (см. табл. 26 и 27), то сжатой ненапрягаемой арматуры по расчету не требуется. В этом случае площадь сечения напрягаемой арматуры в растянутой зоне при известной площади ненапрягаемой растянутой арматуры Аs (например, принятой из конструктивных соображений) определяется по формуле

, (31)

где значение z и значение x , необходимое для вычисления g s6 (см. п. 3.7), определяются по табл. 28 в зависимости от a m .

Если a m > a R , то требуется увеличить сечение или повысить класс бетона, или установить сжатую ненапрягаемую арматуру согласно п. 3.12.

П р и м е ч а н и е. При ненапрягаемой арматуре с физическим пределом текучести, когда выполняется условие Rs As > 0,2 Rs Asp , значения x R и a R определяются по ненапрягаемой арматуре.

Таблица 28

x ( x R )

z

a m ( a R )

x ( x R )

z

a m ( a R )

0,01

0,995

0,010

0,39

0,805

0,314

0,02

0,99

0,020

0,40

0,8

0,32

0,03

0,985

0,030

0,41

0,795

0,326

0,04

0,98

0,039

0,42

0,79

0,332

0,05

0,975

0,049

0,43

0,785

0,338

0,06

0,97

0,058

0,44

0,78

0,343

0,07

0,965

0,068

0,45

0,775

0,349

0,08

0,96

0,077

0,46

0,77

0,354

0,09

0,955

0,086

0,47

0,765

0,360

0,10

0,95

0,095

0,48

0,76

0,365

0,11

0,945

0,104

0,49

0,755

0,37

0,12

0,94

0,113

0,50

0,75

0,375

0,13

0,935

0,122

0,51

0,745

0,38

0,14

0,93

0,13

0,52

0,74

0,385

0,15

0,925

0,139

0,53

0,735

0,39

0,16

0,92

0,147

0,54

0,73

0,394

0,17

0,915

0,156

0,55

0,725

0,399

0,18

0,91

0,164

0,56

0,72

0,403

0,19

0,905

0,172

0,57

0,715

0,407

0,20

0,9

0,18

0,58

0,71

0,412

0,21

0,895

0,188

0,59

0,705

0,416

0,22

0,89

0,196

0,60

0,7

0,42

0,23

0,885

0,204

0,62

0,69

0,428

0,24

0,88

0,211

0,64

0,68

0,435

0,25

0,875

0,219

0,66

0,67

0,442

0,26

0,87

0,226

0,68

0,66

0,449

0,27

0,865

0,234

0,70

0,65

0,455

0,28

0,86

0,241

0,72

0,64

0,461

0,29

0,855

0,248

0,74

0,63

0,466

0,30

0,85

0,255

0,76

0,62

0,471

0,31

0,845

0,262

0,78

0,61

0,476

0,32

0,84

0,269

0,80

0,6

0,48

0,33

0,835

0,276

0,85

0,575

0,489

0,34

0,83

0,282

0,90

0,55

0,495

0,35

0,825

0,289

0,95

0,525

0,499

0,36

0,82

0,295

1,00

0,50

0,5

0,37

0,815

0,302

-

-

-

0,38

0,81

0,308




Для изгибаемых элементов прямоугольного сечения :

;

;

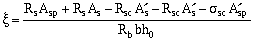a m = x (1 - 0,5 x ) ; z = 1 - 0,5 x .

3.12. Требуемая площадь сечения сжатой ненапрягаемой арматуры при известной площади напрягаемой арматуры А ¢ sp (например, принятой из условия ограничения начальных трещин) определяется по формуле

; (32)

Если принятая площадь сечения сжатой ненапрягаемой арматуры близка к ее значению А's , вычисленному по формуле (32), то требуемая площадь сечения напрягаемой арматуры растянутой зоны определяется по формуле

, (33)

где x R - см. п. 3.6, а также примечание к п. 3.11.

Если принятая площадь сечения сжатой арматуры A's значительно превышает ее требуемое значение из формулы (32), то площадь сечения напрягаемой арматуры растянутой зоны определяется с учетом фактического значения А's .

В любом случае при наличии учитываемой в расчете арматуры S' требуемая площадь сечения напрягаемой арматуры растянутой зоны определяется по формуле

, (34)

где x - определяется по табл. 28 в зависимости от значения

; (35)

g s6  — см. п. 3.7, при этом должно выполняться условие x < x R (см. табл. 26 и 27).

Если a m < 0, значение Аsp определяется по формуле

, (36)

где h - см. п. 3.7.

ТАВРОВЫЕ И ДВУТАВРОВЫЕ СЕЧЕНИЯ

3.13 (3.16). Расчет сечений, имеющих полку в сжатой зоне (тавровых, двутавровых и т.п.) и арматуру, сосредоточенную у растянутой и у сжатой граней элемента (черт. 6), производится в зависимости от положения границы сжатой зоны:

а) если граница сжатой зоны проходит в полке (черт. 6, а), т.е. соблюдается условие

g s6 Rs Asp + Rs As £ Rb b ¢ f h ¢ f + Rsc A ¢ s + s sc A ¢ sp , (37)

где g s6 определяется по формуле (23) при x = h ¢ f / h0 , расчет производится как для прямоугольного сечения шириной b'f в соответствии с указаниями п. 3.9;

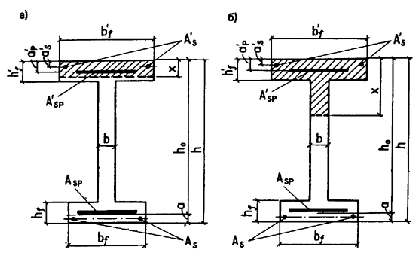
Черт. 6. Форма сжатой зоны в двутавровом поперечном сечении
железобетонного элемента

а - при расположении границы сжатой зоны в полке; б - то же, в ребре

б) если граница сжатой зоны проходит в ребре (черт. 6, б), т.е. условие (37) не соблюдается, то расчет производится следующим образом в зависимости от относительной высоты сжатой зоны x 1 :

; (38)

при x 1 £ x R - из условия

M £ Rb bx (h0 - 0,5x) + Rb (b ¢ f - b) h ¢ f (h0 - 0,5h ¢ f ) + Rsc A ¢ s (h0 - a ¢ s ) +

+ s sc A ¢ s (h0 - a ¢ p ) , (39)

где . (40)

Здесь g s6 определяется по формуле

, (41)

где ;

h - см. п. 3.7;

при x 1 > x R — из условия

M £ Rb b h0 2 + Rb (b ¢ f - b) h ¢ f (h0 - 0,5h ¢ f ) + Rsc A ¢ s (h0 - a ¢ s ) +

+ s sc A ¢ sp (h0 - a ¢ p ) , (42)

при напрягаемой арматуре растянутой зоны классов А-IIIв и А-III значение в условии (42) заменяется на a R ; a R и a m  — см. п. 3.9 или табл. 28.

При большом количестве в растянутой зоне ненапрягаемой арматуры с физическим пределом текучести (когда Rs As > 0,2Rs Asp ) следует учитывать указания п. 3.9.

П р и м е ч а н и я: 1. При переменной высоте свесов полки допускается принимать значение h ¢ f равным средней высоте свесов.

2. Ширина сжатой полки b'f , вводимая в расчет, не должна превышать значений, указанных в п. 3.16.

3.14. Требуемая площадь сечения сжатой ненапрягаемой арматуры определяется по формуле

, (43)

где a R  — определяется по формуле a R = x R (1 - 0,5 x R );

x R  — см. п. 3.6.

При этом, если x R £ h'f / h0 , значение A's определяется как для прямоугольных сечений шириной b = b'f согласно п. 3.12.

3.15. Требуемая площадь сечения напрягаемой арматуры, расположенной в растянутой зоне, определяется следующим образом:

а) если граница сжатой зоны проходит в полке, т.е. соблюдается условие

М £ Rb b'f h'f (h 0 - 0,5 h'f ) + Rsc A ¢ s (h0 - a's ) + s sc A ¢ sp (h0 - a'p ) , (44)

площадь сечения растянутой арматуры определяется как для прямоугольного сечения шириной b ¢ f в соответствии с указаниями пп. 3.11 и 3.12;

б) если граница сжатой зоны проходит в ребре, т.е. условие (44) не соблюдается, площадь сечения растянутой напрягаемой арматуры определяется по формуле

, (45)

где x  — определяется по табл. 28 в зависимости от значения

;

(46)

g s6 - см. п. 3.7.

При этом должно соблюдаться условие x £ x R , где x R  — см. п. 3.6 и табл. 26 и 27, а также примечание к п. 3.11.

3.16 (3.16). Вводимая в расчет ширина сжатой полки b ¢ f принимается из условия, что ширина свеса в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:

а) при наличии поперечных ребер или при h ¢ f ³ 0,1h  — 1/2 расстояния в свету между продольными ребрами;

б) при отсутствии поперечных ребер или при расстояниях между ними б ó льших, чем расстояния между продольными ребрами, и h'f < 0,1h - 6h'f ;

в) при консольных свесах полки:

при h ¢ f ³ 0,1h ................................................. 6h ¢ f

„ 0,05h £ h ¢ f < 0,1h .................................... 3 h ¢ f

„ h'f < 0,05h ................... свесы не учитываются

Примеры расчета

Прямоугольные сечения

Пример 3. Дано: размеры сечения — b = 300 мм, h = 700 мм; а = 50 мм; нагрузки непродолжительного действия отсутствуют; бетон тяжелый класса В25 (Rb = 13 МПа при g b2 = 0,9); напрягаемая арматура класса A-IV (Rs = 510 МПа), площадью сечения Аsр = 1847 мм2 (3 Æ 28); предварительное напряжение при g sp < 1: без учета потерь s sp1 = 500 МПа, с учетом всех потерь s sp2 = 400 МПа; ненапрягаемая арматура класса А-Ш (Rs = 365 МПа), площадью сечения Аs = 236 мм2 (3 Æ 10); изгибающий момент М = 580 кН × м; натяжение арматуры электротермическое автоматизированное.

Требуется проверить прочность сечения.

Р а с ч е т. h0 = 700 — 50 = 650 мм. По формуле (24) определим значение x 1 :

.

Поскольку натяжение арматуры класса A-IV электротермическое автоматизированное, определим значение Ds sp согласно п. 3.6:

Ds sp = 1500 s sp1 / Rs - 1200 = 1500 × 500/510 - 1200 = 270 МПа > 0.

Из табл. 26 при g b2 = 0,9, классе арматуры A-IV, классе бетона В25 и при = 1,31 находим x R = 0,65.

Поскольку x 1 = 0,405 < x R = 0,65, расчет ведем из условия (25), определяя высоту сжатой зоны х по формуле (26).

Так как сечение прямоугольное, то коэффициент g s6 вычисляем по формуле (23) при x = 0,405 и h = 1,2:

g s6 = h - ( h - 1) = 1 ,2 - 0,2 = 1,15 < h = 1,2.

Тогда: = 300 мм ;

Rb bx(h 0 - 0,5x) = 13 × 300 × 300(650 - 0,5 × 300) =

= 585 × 106 Н × мм = 585 кН × м > М = 580 кН × м,

т.е. прочность сечения обеспечена.

Пример 4. Дано: размеры сечения - b = 300 мм, h = 700 мм; a = 60 мм, a ¢ p = 30 мм; бетон тяжелый класса В30 (Rb = 15,5 МПа при g b2 = 0,9); напрягаемая арматура класса Вр-II, диаметром 5 мм (Rs = 1050 МПа); ненапрягаемая арматура класса А-III (Rs = 365 МПа); площадь сечения арматуры S : Аsр = 1570 мм2 (80 Æ 5) и Аs = 236 мм2 (3 Æ 10); площадь сечения арматуры S' - А'sр = 392 мм2 (20 Æ 5); предварительное напряжение с учетом всех потерь: для арматуры S при g sp < 1 — s sp = 630 МПа, для арматуры S' при g sp > 1 - s 'sp = 880 МПа; натяжение арматуры механическое; изгибающий момент М = 650 кН × м.

Требуется проверить прочность сечения.

Р а с ч е т. h 0 = 700 — 60 = 640 мм. Определяем напряжение в предварительно напряженной арматуре сжатой зоны s sc согласно п. 3.8.

Так как g b2 = 0,9, принимаем s sc,u = 500 МПа (см. п. 3.6).

s sc = s sc,u - s 'sp = 500 - 880 = - 380 МПа.

Из формулы (24) определим значение x 1 :

= 0,634.

Поскольку напрягаемая арматура класса Вр-II , принимаем значение Ds sp = 0 (см. п. 3.6).

Из табл. 26 при g b2 > 0, 9, классе арматуры Вр-II, классе бетона В30 и ( s sp + Ds sp ) / Rs = 630 / 1050 = 0,6 находим значение x R = 0,46.

Так как x 1 = 0,634 > x R = 0,46, прочность сечения проверяем из условия (28).

Из табл. 28 находим при x = x 1 = 0,634 a m = 0,433, а при x R = 0,46 a R = 0,354.

Тогда 15 ,5 × 300 × 6402 -

- 380 × 392(640 - 30) = 660 × 106 Н × мм = 660 кH × м > М = 650 кН × м,

т.е. прочность сечения обеспечена.

Пример 5. Дано: размеры сечения — b = 300 мм, h = 700 мм, а = a ¢ s = 50 мм; бетон тяжелый класса В25 (Rb = 13 МПа при g b2 = 0,9); напрягаемая арматура S класса A-IV (Rs = 510 МПа); ненапрягаемая арматура S' класса А-III (Rsc = 365 МПа), площадью сечения A ¢ s = 804 мм2 (1 Æ 32); изгибающий момент М = 500 кН × м.

Требуется определить площадь сечения продольной напрягаемой арматуры.

Р а с ч е т. h0 = 700 — 50 = 650 мм. Площадь сечения продольной напрягаемой арматуры, расположенной в растянутой зоне, определяем согласно п. 3.12. По формуле (35) вычисляем значение a m :

= 0,198 .

Из табл. 28 по значению a m = 0,198 находим x = 0,223. Из табл. 26 при g b2 = 0, 9, классе арматуры A-IV, классе бетона В25, принимая, согласно примеч. 1, ( s sp + Ds sp ) / Rs = 0,6, находим значение x R = 0,54.

Поскольку x = 0,223 < x R = 0,54, то площадь сечения арматуры определяем по формуле (34).

Так как x = 0,223 < 0,5 x R = 0,5 × 0,54 = 0,27, то, согласно п. 3.7, g s6 = h = 1,2.

Отсюда

= 1410 мм2 .

Принимаем в сечении 3 Æ 25 (Asp = 14 73 мм2 ).

Тавровые и двутавровые сечения

Пример 6. Дано: размеры сечения — b'f = 1120 мм, h'f = 30 мм, b = 100 мм, h = 300 мм, a = 30 мм; бетон тяжелый класса В25 (Rb = 13 МПа при g b2 = 0,9); предварительно напряженная арматура класса A-IV (Rs = 510 МПа); изгибающий момент = 23 кН × м.

Требуется определить площадь сечения арматуры.

Р а с ч е т. h0 = 300 - 30 = 270 мм. Расчет ведем, согласно указаниям п. 3.15, в предположении, что сжатой ненапрягаемой арматуры не требуется. Проверяем условие (44):

Rb b'f h'f (h0 - 0,5h ¢ f ) = 13 × 1120 × 30 (270 - 0,5 × 30) = 111,4 кН × м > M = 23 кН × м, т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b = b ¢ f = 1120 мм согласно п. 3.11.

Определим значение a m по формуле (30):

= 0,0217 .

Из табл. 26 при g b2 = 0,9, классе арматуры A-IV, классе бетона В25, принимая, согласно примеч. 1, ( s sp + Ds sp ) / Rs = 0,6, находим x R = 0,54. Тогда из табл. 28 при x R = 0,54 a R = 0,394.

Так как a m = 0,0217 < a R = 0,394, сжатой арматуры не требуется, и площадь сечения арматуры S вычисляем по формуле (31). Для этого по табл. 28 при a m = 0,0217 находим z = 0,989 и x = 0,022.

Так как x = 0,022 < 0,5 x R = 0,5 × 0,54 = 0,27, то, согласно п. 3.7, g s6 = h = 1,2.

Тогда при Аs = 0

= 140 мм2 .

Принимаем 1 Æ 14 (Аs р = 154 мм2 ).

Пример 7. Дано: размеры сечения — b'f = 280 мм, h'f = 200 мм, b = 80 мм, h = 900 мм, a = 72 мм, a' = 40 мм; бетон тяжелый класса В30 (Rb = 15,5 МПа при g b2 = 0,9); напрягаемая арматура S класса A-IV (Rs = 510 МПа), площадью сечения Аsр = 2036 мм2 (8 Æ 18); ненапрягаемая арматура S' класса А-III (Rsc = 365 МПа), площадью сечения А's = 226 мм2 (2 Æ 12); предварительное напряжение арматуры при g sp < 1: без учета потерь - s sp1 = 380 МПа, с учетом всех потерь - g sp2 = 3 20 МПа; потери по поз. 3—5 табл. 4 отсутствуют; натяжение арматуры механическое; изгибающий момент M = 790 кН × м.

Требуется проверить прочность сечения.

Р а с ч е т. h0 = 900 — 72 = 828 мм. Проверяем условие (37), принимая g s6 = 1:

Rb b'f h'f + Rsc A's = 15,5 × 280 × 200 + 365 × 226 = 950 500 H < g s6 Rs Asp = 1 × 510 × 2036 = 1 038 400 H, т.е. условие (37) не соблюдается; при g s6 > 1 это условие тем более не будет соблюдаться и, следовательно, граница сжатой зоны проходит в ребре, а прочность сечения проверяем согласно п. 3.13б.

Из формулы (38) определим значение

= 0,327 .

Поскольку натяжение арматуры класса A-IV механическое, определим значение Ds sp согласно п. 3.6, принимая s sp1 = 380 МПа:

= - 80 МПа < 0 .

Принимаем Ds sp = 0.

Из табл. 26 при g b2 = 0,9, классе арматуры A-IV, классе бетона В30 и ( s sp + Ds sp ) / Rs = 320 / 510 = 0,627 находим x R = 0,52.

Поскольку x 1 = 0,327 < x R = 0,52, расчет ведем из условия (39) с учетом коэффициента g s6 , определяемого по формуле (41):

= 0,684 ;

h = 1,2 (см. п. 3.7);

=

= 1,082 < h = 1,2.

Высота сжатой зоны равна:

340 мм.

Тогда Rb bx(h 0 - 0,5x) + Rb (b'f - b)h ¢ f (h 0 - 0,5h ¢ f )+ Rsc A ¢ s (h0 - а's ) =

= 15,5 × 80 × 340(828 - 0,5 × 340) + 15,5 × 200 × 200(828 - 0,5 × 200) +

+ 365 × 226(828 - 40) = 795 × 106 Н × мм = 795 кН × м > М= 790 кН × м,

т.е. прочность сечения обеспечена.

Пример 8. Дано: балка покрытия с размерами сечения - b'f = 280 мм, h'f = 200 мм, b = 80 мм, h = 900 мм, a = 90 мм, a ¢ s = 40 мм; бетон тяжелый класса В35; напрягаемая арматура S из канатов класса К-7, диаметром 15 мм (Rs = 1080 МПа); ненапрягаемая арматура S' класса A-III (Rsc = 365 МПа), площадью сечения А ¢ s = 226 мм2 (2 Æ 12); изгибающие моменты: без учета нагрузки от подвесного транспорта MI = 740 кН × м, с учетом нагрузки от подвесного транспорта MII = 1000 кН × м.

Требуется определить площадь сечения напрягаемой арматуры S.

Р а с ч е т. Проверяем условие (19) :

0,82MII = 0,82 × 1000 = 820 кН × м > MI = 740 кН × м, т.е. расчет ведем только по случаю «б» — на действие момента М = МII = 1000 кН × м, принимая Rb = 21,5 МПа при g b2 = 1,1;

h0 = h - a = 900 - 90 = 810 мм.

Проверяем условие (44):

Rb b'f h'f - 0,5h'f ) + Rsc A ¢ s (h0 - a ¢ s ) = 21,5 × 280 × 200(810 - 0,5 × 200) +

+ 365 × 226(810 - 40) = 918 × 106 Н × мм = 918 кН × м < M= 1000 кН × м,

т.е. граница сжатой зоны проходит в ребре, и поэтому требуемую арматуру определяем согласно п. 3.15б.

По формуле (46) определяем значение a m :

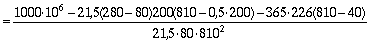= 0,29.

Из табл. 28 при a m = 0,29 находим x = 0,35.

Из табл. 26 при g b2 = 1,1, классе арматуры К-7, классе бетона В35 и ( s sp + Ds sp ) / Rs = 0,6 находим x R = 0,38.

Так как x = 0,35 < x R = 0,38, то сжатой арматуры поставлено достаточно, и площадь сечения арматуры S вычисляем по формуле (45).

Для этого, согласно п. 3.7, определим коэффициент g s6 .

Для арматуры класса К-7 h = 1,15.

= 1,024 < h = 1,15.

Тогда

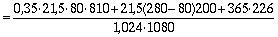= 1293 мм2 .

Принимаем 10 Æ 15 (Аsp = 1416 мм2 ).

ЭЛЕМЕНТЫ, РАБОТАЮЩИЕ НА КОСОЙ ИЗГИБ

3.17. Расчет прямоугольных, тавровых, двутавровых и Г-образных сечений элементов, работающих на косой изгиб, допускается производить, принимая форму сжатой зоны по черт. 7; при этом должно удовлетворяться условие

Мх £ Rb [So n ,x +Aweb (h0 - x 1 /3)] Rsc Ssx + s sc Sspx , (47)

где Мх — составляющая изгибающего момента в плоскости оси х (за оси х и у принимаются две взаимно перпендикулярные оси, проходящие через точку приложения равнодействующей усилий в растянутой арматуре, параллельно сторонам сечения; для сечения с полкой ось х принимается параллельно плоскости ребра);

Aweb = Ab - Ao n ; (48)

Ab  — площадь сжатой зоны бетона, равная:

; (49)

Ao n  — площадь сечения наиболее сжатого свеса полки;

x1  — размер сжатой зоны бетона по наиболее сжатой стороне сечения, определяемый по формуле

x1 = - t + ; (50)

здесь ; (51)

So n ,x  — статический момент площади Аo n в плоскости оси х относительно оси у;

So n ,y  — то же, в плоскости оси у относительно оси x;

b0  — расстояние от равнодействующей усилий в растянутой арматуре до наиболее сжатой боковой стороны сечения (грани ребра);

b  — угол наклона плоскости действия изгибающего момента к оси x, т.e. ctg b =Mx / My ;

Ssx , Sspx  — статические моменты площади сечения соответственно ненапрягаемой и напрягаемой арматуры относительно оси у.

Черт. 7. Форма сжатой зоны в поперечном сечении железобетонного элемента, работающего на косой изгиб

а — таврового сечения; б — прямоугольного сечения; 1-1 — плоскость действия изгибающего момента; 2 — точка приложения
равнодействующей усилий в растянутой арматуре

При расчете прямоугольных сечений значения Ao n , So n ,x и So n ,y в формулах (47), (48) и (51) принимаются равными нулю.

Если Ab < Аo n или если х < 0,2h ¢ f , расчет производится как для прямоугольного сечения шириной b = b'f .

Если выполняется условие

, (52)

где bo n  — ширина наименее сжатого свеса полки,

расчет производится без учета косого изгиба, т.е. по формулам пп. 3.9 и 3.13 на действие момента М = Мx ; при этом следует проверить условие (55), принимая х1 , как при косом изгибе.

Приведенную методику расчета следует применять, если относительная высота сжатой зоны, измеренная по нормали к границе сжатой зоны и определяемая по формуле (53), меньше или равна x R (см. п. 3.6):

, (53)

где bo n  — ширина наиболее сжатого свеса;

q  — угол наклона прямой, ограничивающей сжатую зону, к оси у, значение tg q определяется по формуле

tg q = x1 2 / (2Aweb ), (54)

x1 — для определения x 1 вычисляется по формуле (50) при g s6 = 1,0.

Для проверки условия (47) коэффициент g s6 в формуле (49) определяется, согласно п. 3.7, при значении x , принимаемом равным:

при отсутствии в сжатой зоне полки x = x 1 ;

при наличии в сжатой зоне полки x = ( x 1 + x R ) / 2.

Если выполняется условие

x 1 > x R , (55)

следует произвести повторный расчет с заменой для напрягаемой арматуры в формуле (49) значения g s6 Rs напряжением s s , равным:

для арматуры с условным пределом текучести (см. п. 2.16):

при x £ x el (где x el  — см. п. 3.18 или табл. 31)

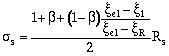; (56)

при x > x el

, (57)

где b - см. п. 3.18;

s sc,u , w , s sp — см. п. 3.6; значение w , а также выражение можно находить по табл. 31 ;

для арматуры с физическим пределом текучести — по формуле (57).

При этом ненапрягаемую арматуру с физическим пределом текучести, если площадь ее сечения не превышает 0,2Asp , допускается учитывать в формуле (49) с полным расчетным сопротивлением. При большей площади указанной ненапрягаемой арматуры, если x > x R (где x R определено для этой арматуры), в формуле (49) значение Rs для ненапрягаемой арматуры заменяется на напряжение s s , определяемое по формуле (57).

Если выполняются условия (58) и (59), то расчет на косой изгиб производится по формулам общего случая расчета нормального сечения согласно п. 3.18:

для прямоугольных и тавровых сечений с полкой в сжатой зоне

x1 > h ; (58)

для двутавровых и тавровых сечений с полкой в растянутой зоне

x1 > h - hf - bo n ,t tg q , (59)

где hf , bo n ,t  — высота и ширина наименее растянутого свеса полки (черт.8).

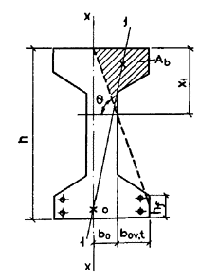
Черт. 8. Двутавровое сечение со сжатой зоной, заходящей
в наименее растянутый свес полки

1-1— плоскость действия изгибающего момента

При использовании формул настоящего пункта за растянутую арматуру площадью Аsp и Аs рекомендуется принимать арматуру, располагаемую вблизи растянутой грани, параллельной оси у, а за сжатую арматуру площадью А'sp и A's - арматуру, располагаемую вблизи сжатой грани, параллельной оси у, но по одну наиболее сжатую сторону от оси х (см. черт. 7).

Если арматура распределена по сечению, что не позволяет до расчета определить площади и центры тяжести сечений арматуры S и S', расчет также производится по формулам общего случая согласно п. 3.18.

При наличии ненапрягаемой арматуры с условным пределом текучести учитывается примечание к п. 3.3.

Примеры расчета

Пример 9. Дано: железобетонный прогон кровли с уклоном 1:4; размеры сечения по черт. 9; класс бетона В25 (Rb = 13 МПа при g b2 = 0,9); арматура S класса A-IV (Rs = 510 МПа) площадью сечению Аsp = 314,2 мм2 (1 Æ 20); арматура S' класса A-III (Rsc = 365 МПа) площадью сечения А ¢ s = 226 мм2 (2 Æ 12); предварительное напряжение арматуры при g sp < 1 с учетом всех потерь s sp = 306 МПа; натяжение арматуры - электротермическое.

Требуется определить предельный изгибающий момент в вертикальной плоскости.

Р а с ч е т ведем без учета стержня, расположенного в наименее сжатом свесе. Из черт. 9 имеем:

h0 = h - а = 300 - 30 = 270 мм; b0 = = 55 мм;

bo n = b ¢ o n = 55 мм; h ¢ f = 60 мм.

Черт. 9. К примеру расчета 9

1-1 — плоскость действия изгибающего момента

Определяем площадь сжатой зоны бетона по формуле (49), учитывая один стержень арматуры S ¢ , т.е. А ¢ s = 113 мм2 (1 Æ 12), и принимая g s6 = 1:

= 9154 мм2 .

Площадь сечения наиболее сжатого свеса и ее статические моменты относительно осей х и у соответственно равны:

Ао n = b'o n h'f = 55 × 60 = 3300 мм2 ;

So n ,y = A о n (b 0 + 0,5b ¢ o n ) = 3300 (55 + 0,5 × 55) = 272 000 мм3 ;

So n ,x = A о n (h0 - 0,5h'f ) = 3300 (270 - 0,5 × 60) = 792 000 мм3

Так как Аb >Аo n , далее расчет производим как для таврового сечения:

Aweb = Ab - Aon = 9154 - 3300 = 5854 мм2 .

Определяем размер сжатой зоны х1 по формуле (50), принимая ctg b = 4:

= 0,9 мм ;

х1 = - t + = 215 ,7 мм .

Проверим условие (52):

= 53,2 мм < х 1 = 215,7 мм,

следовательно, расчет продолжаем по формулам косого изгиба.

Определим значение x 1 по формуле (53), вычислив:

3,97 ;

= 0,614 .

Поскольку натяжение арматуры электротермическое неавтоматизированное, принимаем, согласно п. 3.6, Ds sp = 0.

Из табл. 26 и 31 при g b2 = 0,9, классе арматуры A-IV, классе бетона В25 и при ( s sp + Ds sp ) / Rs = 306/510 = 0,6 находим x R = 0,54 и x el = 0,7.

Поскольку выполняется условие (55):

x 1 = 0,614 > x R = 0,54,

расчет повторяем, заменяя в формуле (49) значение Rs на напряжение s s , определенное по формуле (56).

Согласно п. 3.18, b = 0,8;

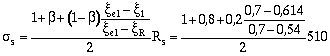= 486 МПа;

= 8574 мм2 ;

Aweb = 8574 - 3300 = 5274 мм2 ;

9 мм ;

х1 = - 9 + = 197 мм .

Определяем предельный изгибающий момент в плоскости оси х из условия (47):

Мх,u = Rb [So n ,x +Aweb (h0 - х1 /3)] + Rsc Ssx = 13[ 792000+5274(270 - 197/3)] +

+ 365 × 113(270 - 20) = 34,6 × 106 Н × мм = 34,6 кН × м.

Предельный изгибающий момент в вертикальной плоскости равен:

= 35,6 кН × м .

ОБЩИЙ СЛУЧАЙ РАСЧЕТА НОРМАЛЬНЫХ СЕЧЕНИЙ
ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ (ПРИ ЛЮБЫХ ФОРМАХ
СЕЧЕНИЯ, НАПРАВЛЕНИЯХ ДЕЙСТВИЯ ВНЕШНЕГО
МОМЕНТА И ЛЮБОМ АРМИРОВАНИИ)

3.18 (3.28). Расчет нормальных сечений изгибаемого элемента в общем случае (черт. 10) выполняется из условия

M £ Rb Sb - Ss si Ssi , (60)

где М — проекция момента внешних сил на плоскость, перпендикулярную прямой, ограничивающей сжатую зону сечения;

Sb  — статический момент площади сжатой зоны бетона относительно оси, параллельной прямой, ограничивающей сжатую зону и проходящей через центр тяжести сечения наиболее растянутого стержня;

Ssi  — статический момент площади сечения i-го стержня продольной арматуры относительно указанной оси;

s si  — напряжение в i-м стержне продольной арматуры.

Черт. 10. Схема усилий и эпюра напряжений в сечении,
нормальном к продольной оси железобетонного элемента,
в общем случае расчета по прочности

1-1 - плоскость, параллельная плоскости действия изгибающего момента; 1 - точка приложения равнодействующих усилий в сжатой арматуре и в бетоне сжатой зоны; 2 - точка приложения равнодействующей усилий в растянутой арматуре

Высота сжатой зоны х и напряжения s si определяются из совместного решения уравнений:

Rb Ab = Ss si Asi , (61)

при x i £ x Ri

, (62)

где h - см. п. 3.7;

при x el,i ³ x i > x Ri

; (63)

при x i > x el,i

. (64)

↑
Закрыть

Строительный каталог