• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11

Для продольной арматуры с физическим пределом текучести (см. п. 2.16) при x _i > x _Ri используется только уравнение (64).

В формулах (61) - (64):

A_b  — площадь сжатой зоны бетона;

A_si  — площадь сечения i-го стержня продольной арматуры;

x _i  —относительная высота сжатой зоны, равная:

,

где h_{0 i} - расстояние от оси, проходящей через центр тяжести сечения рассматриваемого i-го стержня арматуры и параллельной прямой, ограничивающей сжатую зону, до наиболее удаленной точки сжатой зоны сечения (см. черт. 10);

x _Ri , x _el,i - относительная высота сжатой зоны, отвечающая достижению в рассматриваемом стержне напряжений, соответственно равных R_si и b R_si , значение x _Ri определяют по формуле (21) п. 3.6, значение x _el,i — также по формуле (21), принимая

s _sR = b R_si - s _spi , (65)

здесь b - коэффициент, принимаемый равным:

при механическом, а также автоматизированных электротермическом и электротермомеханическом способах натяжения арматуры классов A-IV, A-V, A-VI

, (66)

где s _sp1i - определяется при g _sp < 1,0 (см. п. 1.18) с учетом потерь по поз. 3—5 табл. 4;

s _sc,u , w - см. п. 3.6;

при иных, кроме указанных выше, способах натяжения арматуры классов A-IV, A-V и A-VI, а также для арматуры классов В-II, Вр-II, К-7 и К-19 при любых способах натяжения b = 0,8.

Напряжения s _si , определенные по формуле (64), вводятся в расчет со своими знаками; при этом напряжения со знаком «плюс» означают растягивающие напряжения, а напряжения со знаком «минус» — сжимающие. Напряжения s _si принимаются не менее - R_sc (максимальное сжимающее напряжение) и не менее s _sp  — s _sc,u .

Напряжение s _spi в формуле (64) определяется при коэффициенте g _sp < 1,0, если рассматриваемый стержень расположен в растянутой зоне, и g _sp > 1,0, если стержень расположен в сжатой зоне.

Для определения положения границы сжатой зоны при косом изгибе (т.е. когда плоскость действия момента не перпендикулярна прямой, ограничивающей сжатую зону) кроме использования формул (61)-(64) требуется соблюдение условия параллельности плоскости действия моментов внешних и внутренних сил.

Если в сечении можно выявить характерную ось (например, ось симметрии или ось ребра Г-образного сечения), то при косом изгибе расчет рекомендуется производить в следующем порядке.

1. Провести две оси х и у соответственно параллельно и перпендикулярно указанной характерной оси через центр тяжести сечения наиболее растянутого стержня.

2. Подобрать последовательными приближениями положение прямой, ограничивающей сжатую зону, при постоянном угле ее наклона q так, чтобы удовлетворялось равенство (61) после подстановки в него значений s _si , определенных по формулам (62)-(64); при этом угол q в первом приближении принять равным углу наклона нулевой линии, определенному как для упругого материала.

3. Определить моменты внутренних сил в плоскости осей х и у соответственно M_x,u и M_{y ,u} .

4. Если оба момента оказываются больше или меньше соответствующих составляющих внешнего момента (М_x и M_y ) , то прочность сечения считается соответственно обеспеченной или необеспеченной.

5. Если один из этих моментов (например, М_у,u ) меньше соответствующей составляющей внешнего момента (M_y ) , а другой момент больше составляющей внешнего момента (т.е. М_x,u > М_s ), то следует задаться другим углом q (б ó льшим, чем ранее принятый) и снова выполнить аналогичный расчет.

Примеры расчета

Пример 10. Дано: железобетонная шпала с размерами расчетного поперечного сечения по оси рельса - по черт. 11; бетон тяжелый класса В40 (R_b = 24 МПа при g _b2 = 1,1); арматура из проволоки класса Вр-II, диаметром 3 мм (R_s = 1215 МПа); предварительное напряжение арматуры при g _sp < 1 s _sp = 975 МПа; изгибающий момент в расчетном сечении М = 26 кН × м.

Требуется проверить шпалу на прочность.

Черт. 11. К примеру расчета 10

Р а с ч е т. В связи с распределенным характером расположения арматуры по сечению расчет производим по общему случаю согласно п. 3.18.

По формуле (21) п. 3.6 определяем значения x _R и x _el . Для этого вычислим w = 0,85 - 0,008 R_b = 0,85 - 0,008 × 24 = 0,658. Поскольку арматура проволочная, принимаем Ds _sp = 0 и b = 0,8, s _sc,u = 400 МПа (так как g _b2 = 1,1).

Значение s _sR равно:

при вычислении x _R

s _sR = R_s + 400 - s _sp = 1215 + 400 - 975 = 640 МПа;

при вычислении x _el

s _sR = b R_s - s _sp = 0,8 × 1215 - 975 = - 3 МПа.

Отсюда имеем:

.

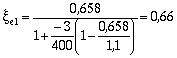Задавшись высотой сжатой зоны х, определим напряжение s _si каждого горизонтального ряда спаренных проволок по формулам (62)-(64) :

при x _i £ x _R

;

при x _el ³ x _i > x _R

= 1640 - 1010 x ;

при x _i > x _el

.

Затем определим сумму усилий во всех рядах проволок Ss _si A_si , где A_si принимается равной площади сечения арматуры в одном i-м ряду, параллельном нейтральной оси.

В первом приближении значение х определим из уравнения (61), принимая среднее напряжение в арматуре равным 0,9R_s = 0,9 × 1215 = 1093 МПа;

S A_si = 367 мм² (52Æ 3),

отсюда = 16700 мм² .

Поскольку сжатая зона имеет трапециевидную форму, высоту сжатой зоны х определим из уравнения (см. черт. 11)

откуда =

= 87,5 мм.

Вычисления приводим в табличной форме (табл. 28а).

Таблица 28а

Окончание табл. 28а

Исходя из вычисленного значения Ss _si A_si (с учетом х = 87,5 мм), вновь определяем:

12900 мм² ;

х = - 313 + 70 мм < 87,5 мм ,

т.е. значение х в первом приближении принято завышенным.

Во втором приближении значением принимаем равным 76 мм и производим аналогичный расчет (см. табл. 28а) :

14450 мм² ;

х = - 313 + 78 мм » 76 мм ,

т.е. значение х = 76 мм принято правильно.

Определим статический момент сжатой зоны бетона в виде трапеции относительно нижнего ряда проволок S_b . Ширина сечения по границе сжатой зоны равна:

b₂ = 167 + 2 × 0,267 × 76 = 208 мм; b₁ = 167 мм.

Тогда S_b =

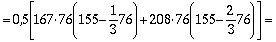1 ,65 × 10⁶ мм³ .

Момент усилия в арматуре относительно центра тяжести нижнего ряда проволок определим по формуле

S s _si S_si = S s _si A_si (h₀₁ - h_oi ) .

Вычисление S s _si S_si приведено в табл. 28а.

Проверяем условие (60):

R_b S_b - S s _si S_si = 24 × 1,65 × 10⁶ - 11,9 × 10⁶ = 27,7 × 10⁶ Н × мм =

= 27,7 кН × м > М = 26 кН × м,

т.е. прочность шпалы обеспечена.

РАСЧЕТ СЕЧЕНИЙ, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА

3.19 (3.29). Расчет элементов по наклонным сечениям должен производиться для обеспечения прочности:

на действие поперечной силы по наклонной полосе между наклонными трещинами - согласно п. 3.21;

на действие поперечной силы по наклонной трещине для элементов с поперечной арматурой — согласно пп. 3.22—3.29, для элементов без поперечной арматуры — согласно п. 3.30;

на действие изгибающего момента по наклонной трещине — согласно пп. 3.31—3.34.

Расчет элементов с поперечной арматурой на действие поперечной силы, согласно пп. 3.22—3.29, не производится, если выполняются условия прочности п. 3.30. При соблюдении этих условий поперечная арматура определяется конструктивными требованиями (см. пп. 5.41 и 5.42).

П р и м е ч а н и е. В настоящем Пособии под поперечной арматурой имеются в виду хомуты и отогнутые стержни (отгибы). Термин «хомуты» включает в себя поперечные стержни сварных каркасов и хомуты вязаных каркасов.

3.20. Расстояния между хомутами s, между опорой и концом отгиба, ближайшего к опоре, s₁ , а также между концом предыдущего и началом последующего отгиба s₂ (черт. 12) должны быть не более величины

, (67)

где j _n  — см. п. 3.22;

j _b4  — см. табл. 29.

Кроме того, эти расстояния должны удовлетворять конструктивным требованиям пп. 5.42 и 5.44.

Черт. 12. Расстояния между хомутами и отгибами

РАСЧЕТ НА ДЕЙСТВИЕ ПОПЕРЕЧНОЙ СИЛЫ
ПО НАКЛОННОЙ СЖАТОЙ ПОЛОСЕ

3.21 (3.30). Расчет элементов на действие поперечной силы для обеспечения прочности по наклонной полосе между наклонными трещинами должен производиться из условия

Q £ 0,3 j _w1 j _b1 R_b b h₀ , (68)

где Q - поперечная сила, принимаемая на расстоянии от опоры не менее h₀ ;

j _w1  — коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, и определяемый по формуле

j _w1 = 1 + 5 am _w , (69)

но не более 1,3;

;

j _b1  — коэффициент, определяемый по формуле

j _b1 = 1 - b R_b , (70)

b  — коэффициент, принимаемый равным для бетона:

тяжелого и мелкозернистого ....... 0,01

легкого ......................................... 0,02

R_b  — в МПа.

При линейном изменении ширины b по высоте в расчет [в формулы (67), (68) и последующие] вводится ширина сечения на уровне середины высоты сечения без учета полок.

РАСЧЕТ НА ДЕЙСТВИЕ ПОПЕРЕЧНОЙ СИЛЫ
ПО НАКЛОННОЙ ТРЕЩИНЕ

Элементы постоянной высоты, армированные хомутами
без отгибов

3.22. Проверка прочности наклонного сечения на действие поперечной силы по наклонной трещине (черт. 13) производится из условия

Q £ Q_b + q_sw c₀ , (71)

где Q — поперечная сила от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения; при вертикальной нагрузке, приложенной к верхней грани элемента, значение Q принимается в нормальном сечении, проходящем через наиболее удаленный от опоры конец наклонного сечения; при нагрузке, приложенной к нижней грани элемента или в пределах высоты его сечения, также допускается значение Q принимать в наиболее удаленном от опоры конце наклонного сечения, если хомуты, установленные на действие отрыва¹ , не учитываются в данном расчете; при этом следует учитывать возможность отсутствия временной нагрузки на участке в пределах наклонного сечения;

¹ Расчет на отрыв производится согласно п. 3.97 «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры» (М., ЦИТП Госстроя СССР, 1986).

Черт. 13. Схема усилий в наклонном сечении элемента, армированного хомутами без отгибов, при расчете его на действие поперечной силы

Q_b  — поперечное усилие, воспринимаемое бетоном и равное:

. (72)

Здесь M_b = j _b2 (1 + j _f + j _n ) R_bt b h₀ ² ; (73)

j _b2  — коэффициент, учитывающий вид бетона и определяемый по табл. 29;

j _f  — коэффициент, учитывающий влияние сжатых полок и определяемый по формуле

, но не более 0,5 ; (74)

при этом величина (b ¢ _f - b) принимается не более 3h ¢ _f ,

учет полок производится, если поперечная арматура в ребре заанкерена в полке, где расположена поперечная арматура, соединяющая свесы полки с ребром;

j _n  — коэффициент, учитывающий влияние предварительного напряжения арматуры растянутой зоны и определяемый по формуле

, (75)

где P = s _sp A_sp - s _s A_s ; суммарный коэффициент 1 + j _f + j _n принимается не более 1,5;

с - длина проекции наклонного сечения на продольную ось элемента.

Таблица 29

Значение Q_b принимается не менее

Q_b,min = j _b3 (1 + j _f + j _n ) R_bt b h₀ (j _b3 - см. табл. 29);

q_sw  — усилие в хомутах на единицу длины элемента в пределах наклонного сечения, определяемое по формуле

q_sw = ; (76)

c₀  — длина проекции наклонной трещины на продольную ось элемента, принимаемая равной:

c₀ = , (77)

но не более с и не более 2h₀ , а также не менее h₀ , если с > h₀ .

При этом для хомутов, устанавливаемых по расчету (т.е. когда не выполняются условия п. 3.30), должно удовлетворяться условие

q_sw ³ . (78)

Разрешается не выполнять условие (78), если в формуле (73) учитывать такое уменьшенное значение R_bt b, при котором условие (78) превращается в равенство, т.е. если принимать М_b = 2 h₀ ² q_sw ; в этом случае всегда с₀ = 2h₀ , но не более с.

При проверке условия (71)в общем случае задаются рядом наклонных сечений при различных значениях с, не превышающих расстояния от опоры до сечения с максимальным изгибающим моментом, а также значения ( j _b2 / j _b3 ) h₀ .

При действии на элемент сосредоточенных сил значения с принимаются равными расстояниям от опоры до точек приложения этих сил (черт. 14).

Черт. 14. Расположение невыгоднейших наклонных сечений при
действии на элемент сосредоточенных и прерывистых нагрузок

1-1 и 2-2 - наклонные сечения, проверяемые на действие соответственно сил Q₁ и Q₂

При расчете элемента на действие равномерно распределенной нагрузки q значение с принимается равным , а если q₁ > 0,56q_sw , следует также принимать с = , где значение q₁ определяется следующим образом:

а) если равномерно распределенная нагрузка q всегда сплошная — q₁ = q,

б) если нагрузка q включает в себя временную эквивалентную равномерно распределенную нагрузку n (т.е. временная нагрузка несплошная, а эпюра моментов М от принятой в расчете нагрузки v всегда огибает эпюру М от любой фактической временной нагрузки) — q₁ = g + n /2 (g  — постоянная сплошная нагрузка).

При этом значение Q принимается равным Q_max - q₁ c (Q_max  — поперечная сила в опорном сечении).

3.23. Определение требуемой интенсивности хомутов, выражаемой через qfw (см. п. 3.22), производится следующим образом:

а) при действии на элемент сосредоточенных сил, располагаемых на расстояниях с_i от опоры, для каждого наклонного сечения с длиной проекции c_i , не превышающей расстояния до сечения с максимальным изгибающим моментом, значение q_sw определяется в зависимости от коэффициента x_i = (где Q_bi  — см. п. 3.22) по одной из следующих формул:

при x_i < x_0i = q_sw(i) = ; (79)

при x_0i £ x_i £ q_sw(i) = ; (80)

при q_sw(i) = ; (81)

при x_i > q_sw(i) = (82)

(здесь h₀ принимается не более с_i ).

Окончательно принимается наибольшее значение q_sw(i) .

В формулах (79) - (82) :

Q_i - поперечная сила в нормальном сечении, расположенном на расстоянии с_i от опоры;

c₀ - принимается равным с_i , но не более 2h₀ ;

б) при действии на элемент только равномерно распределенной нагрузки q требуемая интенсивность хомутов определяется по формулам:

при Q_max £ ; (83)

при ; (84)

в обоих случаях q_sw принимается не менее ;

при Q_max > q_sw = . (85)

В случае, если полученное значение q_sw не удовлетворяет условию (78), следует снова вычислить q_sw по формуле

,

где Q_b1 = ;

Q_max - поперечная сила в опорном сечении;

M_b , q₁ , j _b2 , j _b3 - см. п. 3.22.

3.24. При уменьшении интенсивности хомутов от опоры к пролету с q_sw1 на q_sw2 (например, увеличением шага хомутов) следует проверить условие (71) при значениях с, превышающих l₁ - длину участка элемента с интенсивностью хомутов q_sw1 (черт. 15). При этом выражение q_sw c₀ заменяется:

при c - l₁ < c₀₁ на q_sw1 c₀₁ - (q_sw1 - q_sw2 ) (c - l₁ ) ;

при c₀₂ > c - l₁ ³ c₀₁ на q_sw2 (c - l₁ ) ;

при c - l₁ ³ c₀₂ на q_sw2 c₀₂ ,

где значения c₀₁ и c₀₂ определяются по формуле (77) при q_sw , соответственно равном q_sw1 и q_sw2 .

Черт. 15. Изменение интенсивности хомутов в пределах наклонного
сечения

При действии на элемент равномерно распределенной нагрузки длина участка l₁ с интенсивностью q_sw1 определяется следующим образом:

при q₁ > q_sw1 - q_sw2 ,

где , но не более ;

при q₁ £ q_sw1 - q_sw2 .

Здесь q ₁ — см. п. 3.22.

Если для интенсивности q _ыц2 не выполняется условие (78), длина l₁ вычисляется при скорректированных значениях М_b = 2h₀ ² q_sw2 j _b2 / j _b3 и Q_b,min = 2 h₀ q_sw2 ; при этом выражение (Q_b,min + q_sw2 c₀₁ ) принимается не менее нескорректированного значения Q_b,min .

Элементы постоянной высоты, армированные отгибами

3.25. Проверка прочности наклонного сечения на действие поперечной силы для элемента с отгибами производится из условия (71) п. 3.22 с добавлением к правой части условия (71) значения

Q_s,inc = A_s,inc R_sw sin q , (86)

где A_s,inc - площадь сечения отгибов, пересекающих опасную наклонную трещину с длиной проекции c₀ ;

q - угол наклона отгибов к продольной оси элемента.

Значение c₀ принимается равным длине участка элемента в пределах рассматриваемого наклонного сечения, для которого выражение q_sw c₀ + Q_s,inc + М_b / c₀ принимает минимальное значение. Для этого рассматриваются участки от конца наклонного сечения или от конца отгиба в пределах длины с до начала отгиба, более близкого к опоре или до опоры (черт. 16), при этом длина участка принимается не более значения c₀ , определяемого по формуле (77).

Черт. 16. К определению наиболее опасной наклонной трещины
для элементов с отгибами

1, 2, 3 — возможные наклонные трещины; 4-4 — рассматриваемое
наклонное сечение

Наиболее опасная наклонная трещина на черт. 16 соответствует минимальному значению из следующих выражений:

q_sw c₀₁ + R_sw A_s,inc1 sin q ₁ + M_b / c₀₁ ;

q_sw c₀ + R_sw A_s,inc2 sin q ₂ + M_b / c₀ [ здесь с₀ - см. формулу (77)];

q_sw c₀₃ + M_b / c₀₃ .

Значения с принимаются равными расстояниям от опоры до конца отгибов, а также до мест приложения сосредоточенных сил (см. черт. 16), кроме того, следует проверить наклонные сечения, заканчивающиеся на расстоянии с₀ , определяемом по формуле (77), от начала последнего и предпоследнего отгибов.

Элементы переменной высоты с поперечным армированием

3.26 (3.33). Расчет элементов с наклонными сжатыми гранями на действие поперечной силы производится согласно пп. 3.22, 3.24 и 3.25 с учетом указаний пп. 3.27 и 3.28, принимая в качестве рабочей высоты наибольшее значение h ₀ в пределах рассматриваемого наклонного сечения (черт. 17, а, в).

Расчет элементов с наклонными растянутыми гранями на действие поперечной силы допускается производить согласно пп. 3.22, 3.24 и 3.25, также принимая в качестве рабочей высоты наибольшее значение h ₀ в пределах наклонного сечения в растянутой зоне (черт. 17, б).

Черт. 17. Наклонные сечения элементов с переменной высотой сечения

а - балка с наклонной сжатой гранью; б - балка с наклонной растянутой гранью; в - консоль с наклонной сжатой гранью

3.27. Для балок без отгибов с высотой, равномерно увеличивающейся от опоры к пролету (черт. 17, а, б), рассчитываемых на действие равномерно распределенной нагрузки q, наклонное сечение проверяется из условия (71) п. 3.22 при невыгоднейшем значении с, определяемом следующим образом:

если выполняется условие

q₁ < 0,56 q_sw - 2,5 , (87)

значение с вычисляется по формуле

; (88)

если условие (87) не выполняется, значение с вычисляется по формуле

(89)

(при этом c₀ = с),

а также, если q_sw < M_bs / (4 h₀ ² _s ), - по формуле

(90)

(при этом c₀ = 2 h₀ ),

где q_inc = j _b2 (1 + j _fs + j _ns ) R_bt b tg² b ;

M_bs - величина M_b , определяемая по формуле (73) как для опорного сечения балки с рабочей высотой h_{0 s} , без учета приопорного уширения;

b - угол между сжатой и растянутой гранями балки;

j _fs , j _ns - коэффициенты j _f и j _n при h₀ = h_0s .

Рабочая высота h₀ при этом принимается равной h₀ = h_0s + сtg b .

При уменьшении интенсивности хомутов от опоры к пролету следует проверить прочность наклонных сечений, заходящих в участок с меньшей интенсивностью хомутов, учитывая указания п. 3.24.

Участки балки с постоянным характером увеличения рабочей высоты h ₀ не должны быть менее принятого значения с.

При действии на балку сосредоточенных сил проверяются наклонные сечения при значениях с, принимаемых согласно п. 3.22, а также определяемых, если tg b > 0,1, по формуле (89) при q ₁ = 0.

3.28. Для консолей без отгибов с высотой, равномерно увеличивающейся от свободного конца к опоре (черт. 17, в), в общем случае следует проверить условие (71), задаваясь наклонными сечениями со значениями с, определяемыми по формуле (89) при q₁ = 0 и принимаемыми не более расстояния от начала наклонного сечения в растянутой зоне до опоры. При этом за h_0s и Q необходимо принимать соответственно рабочую высоту и поперечную силу в начале наклонного сечения в растянутой зоне. Кроме того, следует проверить наклонные сечения, проведенные до опоры, если при этом с₀ < с.

При действии на консоль сосредоточенных или прерывистых нагрузок начала наклонных сечений располагают в растянутой зоне нормальных сечений, проходящих через концы площадок опирания этих нагрузок (черт. 17, в).

При действии равномерно распределенной нагрузки или нагрузки, линейно увеличивающейся к опоре, консоль рассчитывают так же, как элемент с постоянной высотой сечения, согласно п. 3.22, принимая рабочую высоту h₀ в опорном сечении.

Элементы с поперечным армированием при косом изгибе

3.29. Расчет по поперечной силе элементов прямоугольного сечения, подвергающихся косому изгибу, производится из условия

, (91)

где Q_x , Q_y - составляющие поперечной силы, действующие соответственно в плоскости симметрии х и в нормальной к ней плоскости у в наиболее удаленном от опоры конце наклонного сечения;

Q_{bw (х)} , Q_bw(y)  — предельные поперечные силы, которые могут быть восприняты наклонным сечением при действии их соответственно только в плоскости х и только в плоскости у, принимаемые равными правой части условия (71).

При действии на элемент равномерно распределенной нагрузки допускается определять значения с, согласно п. 3.22, независимо для каждой плоскости х и у.

П р и м е ч а н и е. Отгибы при расчете на поперечную силу при косом изгибе не учитываются.

Элементы без поперечной арматуры

3.30 (3. 32). Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий:

a) Q_max £ 2,5 R_bt b h₀ , (92)

где Q_max -максимальная поперечная сила у грани опоры;

б) Q £ О_b1 , (93)

где Q - поперечная сила в конце наклонного сечения, начинающегося от опоры с длиной проекции с;

Q_b1 - предельная поперечная сила, принимаемая равной M_b /с,
где М_b = j _b4 (1 + j _n ) R_bt b h₀ ² ,

но не менее Q_b,min = j _b3 (1 + j _n ) R_bt b h₀ , (94)

[при этом c = ( j _b4 / j _b3 ) h₀ » 2,5 h₀ ];

j _b3 , j _b4  — см. табл. 29 п. 3.22;

j _n  — см. п. 3.22;

при этом, если в пределах длины с не образуются нормальные трещины [т.е. если М < М_crc , где М_crc определяется по формуле (164) п. 4.2 с заменой R_bt,ser на R_bt ], Q_b1 принимается не менее

Q_crc = , (95)

где S_red - статический момент части приведенного сечения, расположенной по одну сторону от оси, проходящей через центр тяжести сечения, относительно этой оси;

t _xy,crc - касательное напряжение на уровне центра тяжести приведенного сечения, соответствующее образованию наклонных трещин и определяемое из уравнения (183) п. 4.9 с заменой R_bt,ser на R_bt и R_b,ser на R_b ; допускается значение t _xy,crc = t R_bt определять без учета напряжения s _y с помощью графика на черт. 18.

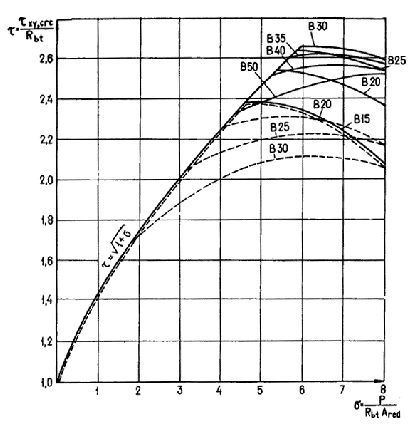
График зависимости t = f ( s )

¾¾ для тяжелого бетона; ----- для мелкозернистого и легкого бетонов

При действии на элемент сосредоточенных или прерывистых нагрузок значения с при проверке условия (93) принимаются равными расстояниям от опоры до начала площадок опирания этих нагрузок (см. черт. 14).

При расчете элемента на действие равномерно распределенной нагрузки значение с принимается равным М_b1 /Q_crc (при этом Q_b1 = Q_crc ), а также равным длине приопорного участка l₁ , где не образуются нормальные трещины (при этом, если l₁ > 2,5 h₀ , то Q_b1 = Q_b,min ) . В обоих случаях принимается Q = Q_max - q₁ c (где q₁ - см. п. 3.22).

РАСЧЕТ НАКЛОННЫХ СЕЧЕНИЙ НА ДЕЙСТВИЕ
ИЗГИБАЮЩЕГО МОМЕНТА

3.31 (3.35). Расчет элементов на действие изгибающего момента для обеспечения прочности по наклонной трещине (черт. 19) должен производиться из условия

М £ (R_s A_sp + R_s A_s ) z_s + S R_sw A_sw z_sw + S R_sw A_s,inc z_s,inc , (96)

где М - момент от внешней нагрузки, расположенной по одну сторону от рассматриваемого наклонного сечения, относительно оси, перпендикулярной плоскости действия момента и проходящей через точку приложения равнодействующей усилий в сжатой зоне (черт. 20);

S R_sw A_sw z_sw , S R_sw A_s,inc z_s,inc - суммы моментов относительной той же оси соответственно от усилий в хомутах и в отгибах, пересекающих растянутую зону наклонного сечения;

z_s , z_sw , z_s,inc - расстояния от плоскостей расположения соответственно продольной арматуры, хомутов и отгибов до указанной выше оси.

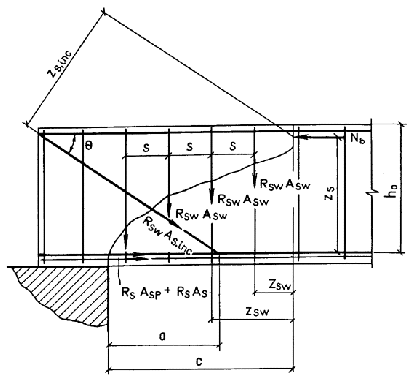
Черт. 19. Схема усилий в наклонном сечении при расчете
по прочности на действие изгибающего момента

Черт. 20. Определение расчетного значения момента
при расчете наклонного сечения

а - для свободно опертой балки; б - для консоли

Высота сжатой зоны наклонного сечения, измеренная по нормали к продольной оси элемента, определяется из условия равновесия проекций усилий в бетоне сжатой зоны и в арматуре, пересекающей растянутую зону наклонного сечения, на продольную ось элемента согласно пп. 3.9 и 3.13. При этом принимается g _s6 = 1,0, а в случае наличия в элементе отгибов в числителе выражения для х добавляется выражение S R_s A_s,inc cos q (где q - угол наклона отгибов к продольной оси элемента).

Величину z_s допускается принимать равной h₀  — 0,5х, но не более h₀ - а ¢ , если значение х вычислено с учетом сжатой арматуры.

Величина S R_sw A_sw z_sw при хомутах постоянной интенсивности определяется по формуле

S R_sw A_sw z_sw = 0,5 q_sw c² , (97)

где q_sw  — см. п. 3.22;

с — длина проекции наклонного сечения на продольную ось элемента, измеренная между точками приложения равнодействующих усилий в растянутой арматуре и в сжатой зоне (см. п. 3.33).

Величина z_s,inc для каждой плоскости отгибов определяется по формуле

z_s,inc = z_s cos q + (с - a) sin q , (98)

где а — расстояние от начала наклонного сечения до начала отгиба в растянутой зоне (см. черт. 19).

3.32. Расчет наклонных сечений на действие момента производится у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров, а также в местах обрыва или отгиба продольной арматуры в пролете.

Кроме того, расчет наклонных сечений на действие момента производится в местах резкого изменения конфигурации элементов (подрезки, узлы и т.п.).

Если наклонное сечение пересекает в растянутой зоне напрягаемую арматуру без анкеров на длине зоны передачи напряжений (см. п. 2.26) или ненапрягаемую арматуру без анкеров на длине зоны анкеровки (см. п. 5.32), значение расчетного сопротивления R_s соответствующей арматуры снижается путем умножения его на коэффициент условий работы g _s3 , определяемый согласно поз. 3 табл. 23.

Расчет наклонных сечений на действие момента не производится, если выполняются условия п. 3.30.

3. 33. Для свободно опертых балок невыгоднейшее наклонное сечение начинается от грани опоры и имеет длину проекции с при постоянной высоте сечения, равную:

(99)

и принимаемую не более l₁  — длины приопорного участка, на котором Q ³ Q._crc (см. п. 3.30) или, если на нем образуются нормальные трещины, Q ³ Q_b1 .

В формуле (99):

Q — поперечная сила в опорном сечении;

F_i , q — сосредоточенная и равномерно распределенная нагрузки в пределах наклонного сечения;

q_sw  — см. формулу (76) п. 3.22;

q  — угол наклона отгибов к продольной оси элемента.

Если значение с, определенное с учетом сосредоточенной силы F_i , оказывается меньше расстояния от грани опоры до этой силы F_i , а определенное без учета силы F_i  — больше этого расстояния, то за значение с следует принимать расстояние до силы F_i .

Если в пределах длины с хомуты изменяют свою интенсивность с q_sw1 у начала наклонного сечения на q_sw2 , то значение с определяется по формуле (99) при q_sw = q_sw2 и при уменьшении числителя на величину (q_sw2 - q_sw2 )l₁ , где l₁ - длина участка с интенсивностью хомутов q_sw1 .

Для балок, нагруженных равномерно распределенной нагрузкой q с постоянной интенсивностью хомутов без отгибов, условие (96) можно заменить условием

• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11