• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11

w = a - 0,008 R_b ^(p) ; ; ; a _R = x _R (1 -x _R /2) .

Если x > x _R , расчетную несущую способность на действие обжатия при необходимости можно несколько увеличить, используя условие (128) при значении х, определяемом следующим образом:

при отсутствии в менее обжатой зоне арматуры с условным пределом текучести

, (130)

где ;

, w  — см. табл. 33;

при наличии в менее обжатой зоне арматуры с условным пределом текучести

, (131)

где x _el  — см. п 3.41в при s _sc,u = 330 МПа;

b  — см. п. 3.18.

При этом, если значение х, определенное по формуле (131), оказывается больше x _el h₀ , то в условие (128) подставляется значение х, определяемое по формуле (130), где и w находят по табл. 33.

Значение е в условиях (128) и (129) определяется согласно п. 3.48.

3.47. Для элементов двутаврового и таврового сечений с полкой в более обжатой зоне (черт. 30) расчет прочности на действие предварительного обжатия производится следующим образом:

если соблюдается условие

N_p £ R_b ^(p) b'_f h'_f - R_s A_sp - R_s A_s + R_sc A'_s (132)

(т.е. граница сжатой зоны проходит в полке), расчет производится как при отсутствии полки в более обжатой зоне в соответствии с п. 3.46 при b = b'_f ;

Черт. 30. Схема усилий в поперечном сечении внецентренно обжатого железобетонного элемента с полкой в сжатой зоне

если условие (132) не соблюдается (т.е. граница сжатой зоны проходит в ребре), расчет производится в зависимости от высоты сжатой зоны

,

а) при [ см. формулу (21) п. 3.6 при s _sc,u = 330 МПа] - из условия

N_p e £ R_b ^(p) bx (h₀ - 0,5x) + R_b ^(p) A_on (h₀ - 0,5h¢ _f ) + R_sc A'_s (h₀ - a¢ _s ), (133)

где e - см. п. 3.48;

б) при x > x _R - из условия

N_p e £ a _R R_b ^(p) bh₀ ² + R_b ^(p) A_on (h₀ - 0,5h¢ _f ) + R_sc A'_s (h₀ - a¢ _s ), (134)

где a _R = (1 - 0,5 x _R );

A_{o n} = (b ¢ _f - b)h ¢ _f  — площадь сечения сжатых свесов.

Значения x _R и a _R при ненапрягаемой арматуре менее обжатой зоны классов А-III и Вр-I можно определять по табл. 33.

Если x > x _R , расчетную несущую способность на действие обжатия при необходимости можно несколько увеличить, используя условие (133) при значении х, определенном по формулам (130) или (131), в которых сила N_p уменьшается на величину R_b ^(p) А_{o n} .

3.48. Значение е в условиях. (128), (129), (133) и (134) определяется по формулам:

при натяжении на упоры

; (135)

при натяжении на бетон

. (136)

В формулах (135) и (136):

М — момент от нагрузок, действующих в стадии изготовления; знак «плюс» принимается, если момент усилия N_p относительно арматуры S и момент М совпадают по направлению, знак «минус» — если направления этих моментов противоположны;

t_0p  — эксцентриситет силы N_p относительно центра тяжести приведенного сечения;

h  — см. пп. 3.39 и 3.45;

у — расстояние от центра тяжести приведенного сечения до наиболее обжатой грани.

Значение в формуле (136) принимается не менее e_a (см. п. 3.35).

Примеры расчета

Пример 20. Дано: ребристая плита покрытия длиной 12 м с поперечным сечением ребра по черт. 31; напрягаемая арматура из канатов класса К-7 натягивается на упоры; предварительное напряжение с учетом первых потерь при g _sp > l s _sp1 = 900 МПа; передаточная прочность тяжелого бетона R_bp = 25 МПа; масса плиты 7,4 т; монтажные петли расположены на расстоянии 800 мм от торца плиты.

Требуется проверить прочность плиты в стадии изготовления.

Черт. 31. К примеру расчета 20

Р а с ч е т. Из черт. 31 видно, что в наиболее обжатой зоне располагается напрягаемая арматура класса К-7, площадью А ¢ _sp = 566 мм² (4 Æ 15). Heнапрягаемую арматуру 1 Æ 5 класса Вр-I , расположенную в этой зоне, в расчете не учитываем, поскольку она не удовлетворяет конструктивным требованиям п. 5.39.

В менее обжатой зоне располагается ненапрягаемая арматура с физическим пределом текучести 1 Æ 10 классов А-III (А_s1 = 78,5 мм² ) и 1 Æ 5 Вр-I +7 Æ 4 Вр-I (А_s2 = 19,6 + 87,9 = 107,6 мм² ).

Поскольку значения R_s для арматуры классов А-III и Вр-I ( Æ 4 и Æ 5) близки, принимаем точку приложения равнодействующей усилий в арматуре менее обжатой зоны в центре тяжести сечения этой арматуры, и тогда расстояние ее от верхней грани сечения равно:

31,6 мм .

Следовательно, h₀ = h - а = 450 - 31,6 = 418 мм.

Из черт. 31 имеем = 55.

Расчетное усилие обжатия, согласно п. 3.44, равно:

N_p = ( s _sp1 - 330)А'_sp = (900 - 330) 566 = 322 600 Н = 322,6 кН.

Определяем значение е согласно п. 3.48. Равномерно распределенная нагрузка от собственного веса плиты, учитывая указания п. 2.14 и коэффициент надежности по нагрузке g _f = 1,1, будет равна:

6,8 кН/м.

Поскольку монтажные петли располагаются на расстоянии l = 0,8 м от торца, невыгоднейший момент от собственного веса, растягивающий верхнюю грань, будет возникать при подъеме плиты. Определим этот момент с учетом коэффициента 1,4 (см. п. 1.9) для половины сечения плиты:

= 1,52 кН × м.

Тогда e = h₀ - a ¢ _p + 368 мм.

Расчетное сопротивление бетона, соответствующее передаточной прочности R_bp = 25 МПа согласно табл. 13 при g _b2 = 1, равно R_b ^(p) = 14,5 МПа, а с учетом коэффициента g _s8 = 1,1 (см. табл. 14, поз. 5) - R_b ^(p) = 1,1 × 14,5 = 16 МПа.

Поскольку ширина ребра b переменна, принимаем в первом приближении ширину ребра посередине высоты сжатой зоны равной x _R h₀ . Из табл. 33 при R_bp = 25 МПа, тяжелом бетоне и проволочной напрягаемой арматуре находим x _R = 0,52. Тогда

= 114 ,2 мм .

Высота сжатой зоны при А_sp = 0 и А'_s = 0 равна:

= 214,2 мм.

Поскольку x = x/h ₀ = 214,2 / 418 = 0,512 < x _R = 0,52, прочность проверяем из условия (128). При этом ширину ребра не пересчитываем, так как полученное значение x близко к x _R :

R_b ^(p) bx (h₀ - 0,5х) = 16 × 114,2 × 214,2 (418 - 0,5 × 214,2) =

= 121,7 × 10⁶ Н × мм = 121,7 кН × м > N_p e = 322,6 × 0, 368 = 118,7 кН × м,

т.е. прочность в стадии изготовления обеспечена.

Центрально-растянутые элементы

3.49 (3.26). При расчете сечений центрально-растянутых железобетонных элементов должно соблюдаться условие

N £ h R_s A_sp,tot + R_s A_s,tot , (137)

где h  — см. п. 3.7;

A_sp,tot , A_s,tot  — площади сечения всей продольной соответственно напрягаемой и ненапрягаемой арматуры.

Внецентренно растянутые элементы

РАСЧЕТ ЭЛЕМЕНТОВ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
ПРИ РАСПОЛОЖЕНИИ ПРОДОЛЬНОЙ СИЛЫ
В ПЛОСКОСТИ СИММЕТРИИ

3.50 (3.27). Расчет прямоугольных сечений внецентренно растянутых элементов с арматурой, сосредоточенной у наиболее растянутой и у сжатой (наименее растянутой) граней, должен производиться в зависимости от положения продольной силы N :

а) если продольная сила N приложена между равнодействующими усилий в арматуре S и S' (черт. 32, а), т.е. при е' £ h ₀ — а ¢ , - из условий:

Ne' £ ( h R_s A_sp + R_s A_s ) (h₀ - а ¢ ); (138)

Ne £ ( h R_s A ¢ _sp + R_s A ¢ _s ) (h₀ - а ¢ ) , (139)

где h  —см. п. 3.7;

при симметричной арматуре используется только условие (138);

б) если продольная сила N приложена за пределами расстояния между равнодействующими усилий в арматуре S и S' (черт. 32, б), т.е. при е' > h ₀ - а ¢ , - из условия

Ne £ R_b bx(h₀ - 0,5x) + R_sc A'_s (h₀ - а ¢ _s ) + s _sc A ¢ _sp (h₀ - a ¢ _p ) , (140)

при этом высота сжатой зоны х определяется по формуле

, (141)

где g _s6 - см. формулу (23); при этом допускается определять из формулы (141) без учета g _s6 ;

s _sc  — см. п. 3.8.

Черт. 32. Схема усилий в прямоугольном сечении внецентренно
растянутого железобетонного элемента при расчете его на прочность

а — продольная сила N приложена между равнодействующими усилий
в арматуре S и S'; б — то же, за пределами расстояния между
равнодействующими усилий в арматуре S и S'

Если полученное из расчета по формуле (141) значение х > x _R h₀ , в условие (140) подставляется х = x _R h₀ , где определяется согласно п. 3.6.

Если х < 0, прочность сечения проверяется из условия (138).

При применении ненапрягаемой арматуры с условным пределом текучести следует учитывать примечание к п. 3.3.

П р и м е ч а н и е. Если при е' > h₀ - а' высота сжатой зоны, определенная без учета ненапрягаемой арматуры S',

меньше 2a ¢ _s , расчетную несущую способность можно несколько увеличить, произведя расчет по формулам (140) и (141) без учета ненапрягаемой арматуры S'.

3.51. Элементы прямоугольного сечения с симметричной арматурой, расположенной в несколько рядов по высоте сечения, рассчитываются при силе N, приложенной между крайними рядами арматуры, из условия

Ne₁ £ h R_s S_sp + R_s S_s , (142)

где e₁  — расстояние от силы N до оси, перпендикулярной направлению эксцентриситета и проходящей через наименее растянутый ряд арматуры;

S_sp, S_s  — статические моменты площади сечения соответственно всей напрягаемой и всей ненапрягаемой арматуры относительно той же оси;

h  — см. п. 3.7.

Если сила N приложена за пределами расстояния между крайними рядами арматуры, расчет производится по формулам общего случая согласно п. 3.53.

3.52. Определение требуемого количества продольной арматуры производится следующим образом:

а) при e' £ h₀ - а' площадь сечения напрягаемой арматуры S и S ¢ определяется соответственно по формулам:

; (143)

; (144)

б) при e' > h₀ - а' площадь сечения напрягаемой арматуры S определяется по формуле

, (145)

где x определяется по табл. 28 в зависимости от значения

; (146)

g _s6  — см. п. 3.7.

При этом должно соблюдаться условие a _m £ a _R = x _R (1 - x _R /2 ) ( x _R  — см. табл. 26 или 27). В противном случае следует увеличить площадь сечения ненапрягаемой арматуры A'_s , повысить класс бетона или увеличить размеры сечения.

Если a _m < 0, площадь сечения напрягаемой арматуры S определяется по формуле (143).

При подборе симметричной напрягаемой арматуры в первом приближении в формулах (145) и (146) принимается A ¢ _sp = 0. При этом, если напряжение s _sc сжимающее (т.e. s _sc > 0), повторный расчет можно не производить.

П р и м е ч а н и е. При e' > h₀ - a ' и при отсутствии напрягаемой арматуры S' необходимое количество напрягаемой арматуры S можно несколько снизить, если значение x , определенное по табл. 28 без учета ненапрягаемой арматуры S', т. e. по значению , оказывается меньше 2a'_s /h₀ . В этом случае площадь сечения напрягаемой арматуры S определяется по формуле

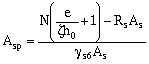, (147)

где значение z и значение x , необходимое для вычисления g _s6 , определяются по табл. 28 в зависимости от .

Общий случай расчета нормальных сечений
внецентренно растянутого элемента
(при любых сечениях, внешних усилиях и любом армировании)

3.53. Расчет нормальных сечений внецентренно растянутого элемента в общем случае (черт. 33) должен производиться из условия

Ne' £ S s _si S_si - R_b S_b , (148)

где e' — расстояние от продольной силы N до оси, параллельной прямой, ограничивающей сжатую зону и проходящей через точку сжатой зоны, наиболее удаленную от указанной прямой;

s _si  — напряжение в 1-м стержне продольной арматуры;

S_si  — статический момент площади сечения i-го стержня продольной арматуры относительно указанной оси;

S_b  — статический момент площади сечения сжатой зоны бетона относительно указанной оси.

Черт. 33. Общий случай расчета внецентренно растянутого элемента

I — точка приложения растягивающей силы N; А — точка приложения равнодействующей усилий в арматуре и бетоне сжатой зоны; Б — точка приложения равнодействующей усилий в арматуре растянутой зоны;
1-6 — арматурные стержни

Высота сжатой зоны бетона х и напряжения s _si определяются из совместного решения уравнений (61)—(64) с добавлением в левую часть формулы (61) значения N.

При косом внецентренном растяжении для определения положения границы сжатой зоны кроме использования формул (61)—(64) требуется соблюдение дополнительного условия, что точки приложения внешней продольной силы, равнодействующей сжимающих усилий в бетоне и арматуре и равнодействующей усилий в растянутой арматуре должны лежать на одной прямой.

Расчет сечений, наклонных к продольной оси элемента

3.54. Расчет наклонных сечений внецентренно растянутых элементов на действие поперечной силы производится как для изгибаемых элементов согласно пп. 3.19-3.30; при этом в случаях, когда N < Р, значение Р в формуле (75) уменьшается на значение продольной силы N, а в случаях, когда N > Р, формула (75) заменяется формулой

, (149)

при этом значение j _n принимается по абсолютной величине не более 0,8. Здесь Р — усилие от предварительного напряжения в арматуре, расположенной в растянутой зоне; при расположении силы N между крайними рядами арматуры учитывается усилие от всей напрягаемой арматуры, кроме арматуры наименее растянутого ряда. В этом случае рабочая высота сечения h₀ отсчитывается от наиболее растянутого ряда.

Расчет наклонных сечений внецентренно растянутых элементов на действие изгибающего момента производится как для изгибаемых элементов согласно пп. 3.31-3.34. При этом высота сжатой зоны в наклонном сечения определяется с учетом растягивающей силы N по формуле (141) или согласно п. 3.53.

Примеры расчета

Внецентренно растянутые элементы

Пример 21. Дано: размеры сечения нижнего пояса безраскосной фермы — b = 220 мм, h = 240 мм, a = a' = 40 мм; бетон класса В30; продольная напрягаемая арматура симметричная класса A-IV (R_s = 510 МПа, h = 1,2), площадью сечения A_sp = А ¢ _sp = 763 мм² (3 Æ 18); продольная растягивающая сила N = 600 кН; максимальный изгибающий момент М = 24 кН•м.

Требуется проверить прочность нормального сечения.

Р а с ч е т. h₀ = h - а = 240 - 40 = 200 мм;

= 0 ,04 м = 40 мм ;

е ¢ = е₀ + 40 = 120 мм .

Так как e' = 120 мм < h ₀ - a' = 200 - 40 = 160 мм, прочность сечения проверяем из условия (138). Условие (139) не проверяем, поскольку арматура симметричная:

h R_s A_sp (h₀ - a ¢ _p ) = 1,2 × 510 × 763 (200 - 40) = 74,7 × 10⁶ H × мм =

= 74,7 кН × м > Ne ¢ = 600 × 0,12 = 72 кН × м,

т.e. прочность сечения обеспечена.

Пример 22. Дано: П-образная плита перекрытия; к нижней грани ее продольного ребра приложена растягивающая сила N = 66 кН, вызванная сдвигающими усилиями в диске перекрытия от ветровых нагрузок; размеры поперечного сечения плиты (для половины сечения) — h = 400 мм, b = 85 мм, b'_f = 350 мм, h'_f = 50 мм, а = 37 мм; бетон класса В25 (R_b = 19 МПа при g _b2 = 1,1 ); продольная растянутая арматура напрягаемая класса A-V (R_s = 680 МПа) и ненапрягаемая класса А-III (R_s = 365 МПа); площади сечения арматуры А_sp = 314 мм² (1 Æ 20) и А_s = 785 мм² (1 Æ 10).

Требуется проверить прочность нормального сечения плиты.

Р а с ч е т. h₀ = h  — а = 400 — 37 = 363 мм. Поскольку сила приложена за пределами расстояния между арматурой S и S', прочность сечения проверяем согласно п. 3.50б.

Предполагая, что граница сжатой зоны проходит в полке, расчет ведем как для прямоугольного сечения (по аналогии с изгибаемыми элементами), принимая b = b'_f = 350 мм. При этом, если х < h ¢ _f , т.е. = 0,138, то x меньше 0,5 x _R (см. табл. 26) и, следовательно, согласно п. 3.7, можно принять g _s6 = h = 1,15.

По формуле (141) определим высоту сжатой зоны х:

=

= 31,3 мм < h ¢ _f = 50 мм ,

т.e. граница сжатой зоны действительно проходит в полке.

Определим Ne - момент внешних сил относительно точки приложения равнодействующей усилий в арматуре S:

Ne = Na + М = 66 × 0,037 + 69 = 71,44 кН × м.

Прочность сечения проверяем из условия (140):

R_b bx (h₀ - 0,5 х) = 19 × 350 × 31,3(363 - 0,5 × 31,3) = 72, 3 × 10⁶ H × мм =
= 72, 3 кН × м > Ne = 71,44 кН × м,

т.е. прочность сечения обеспечена.

Пример 23. Дано: размеры сечения — b = 240 мм, h = 360 мм; расположение продольной напрягаемой арматуры класса A-V (R_s = 680 МПа) — по черт. 34; центрально-приложенная растягивающая сила N = 1000 кН; изгибающий момент М = 80 кН × м; площадь сечения всей продольной арматуры A_sp,tot = 2513 мм² (8 Æ 20).

Черт. 34. К примеру расчета 23

1 - центр тяжести сечения

Требуется проверить прочность нормального сечения.

Р а с ч е т. Расстояние от крайнего ряда арматуры до центра тяжести сечения, согласно черт. 34, равно:

120 мм .

Поскольку e₀ = M / N = 80 / 1000 = 0,08 м = 80 мм < a₁ = 120 мм, сила N приложена между крайними рядами арматуры и прочность сечения можно проверить из условия (142).

Статический момент площади сечения всей арматуры относительно крайнего ряда арматуры равен:

S_sp = А_sp,tot a₁ = 2513 • 120 = 301600 мм³ .

Расстояние от силы N до наименее растянутого ряда арматуры e₁ = e₀ + a₁ = 80 + 120 = 200 мм.

Согласно п. 3.7, h = 1,15 (для арматуры класса A-V);

h R_s S_sp = 1,15 × 680 × 301 600 = 235,85 × 10⁶ H × мм =
= 235,85 кН × м > Ne₁ = 1000 × 0,2 = 200 кН × м,

т. е. прочность сечения обеспечена.

Пример 24. Дано: размеры сечения нижнего пояса подстропильной фермы — b = 550 мм, h = 210 мм, а = а' = 50 мм; продольная напрягаемая арматура в виде канатов класса К-7, диаметром 15 мм (R_s = 1080 МПа); продольная растягивающая сила N = 2200 кН × м; изгибающий момент М = 44 кН × м.

Требуется определить площадь сечения симметричной продольной арматуры.

Р а с ч е т. h ₀ = h - a = 210 - 50 = 160 мм;

e₀ = M / N = 44 / 2200 = 0,02 м = 20 мм;

е' = e₀ + h / 2 - a = 20 + 210 / 2 - 50 = 75 мм.

Так как h₀ - a' = 160 - 50 = 110 мм > е' = 75 мм, площадь сечения арматуры S и S ¢ определяем по формуле (143), принимая h = 1,15:

1208 мм² .

Принимаем A_sp = А'_sp = 1273 мм² (9 Æ 15 К-7).

Пример 25. Дано: размеры сечения нижнего пояса безраскосной фермы — b = 240 мм, h = 360 мм, а = а' = 60 мм; бетон класса В30 (R_b = 15,5 МПа при g _b2 = 0,9); продольная напрягаемая арматура класса A-V (R_s = 680 МПа); растягивающая сила N = 480 кН; изгибающий момент М = 72 кН × м.

Требуется определить площадь сечения симметричной продольной арматуры.

Р а с ч е т. h₀ = h - а = 360 - 60 = 300 мм; е₀ = M / N = 72 / 480 = 0,15 м = 150 мм;

е' = е₀ + h/2 - а ¢ = 150 + 360 / 2 - 60 = 270 мм;

е = е₀ - h/2 + а = 150 - 360/2 + 60 = 30 мм.

Так как h₀ - а ¢ = 300 — 60 = 240 мм < е' = 270 мм, арматуру подбираем согласно п. 3.52б.

Тогда по формуле (145) определяем значение a _m , принимая в первом приближении A'_sp = 0:

= 0,043 .

Из табл. 28 для a _m = 0,043 находим x = 0,045.

Из табл. 26 при g _b2 = 0,9, классе арматуры A-V, классе бетона В30 и ( s _sp + Ds _sp )/R_s = 0,6 (см. примечание к табл. 26) находим x _R = 0,5.

Так как x = 0,045 < 0,5 x _R = 0,25, принимаем g _s6 = h = 1,15.

Площадь сечения арматуры S определяем по формуле (145):

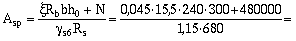678 мм² .

При s¢ _sp = g _sp 0,6R_s = 1,1 × 0,6 × 680 = 449 МПа значение s _sc = s _sc,u -s¢ _sp = 500 — 449 > 0, следовательно, повторный расчет не производим.

Принимаем А_sp = А ¢ _sp = 760 мм² (2 Æ 22).

Пример 26. Дано: элемент нижнего пояса безраскосной фермы с размерами сечения — b = 220 мм, h = 240 мм, a = а ¢ = 40 мм; длина элемента в свету между стойками 2,8 м; бетон тяжелый класса В30 (R_bt = 1,1 МПа при g _b2 = 0,9); поперечная арматура — в виде согнутых сеток из проволоки класса Bp-I (R_sw = 260 МПа при d = 5 мм); продольная центрально-приложенная растягивающая сила N = 300 кН; усилие обжатия от симметрично расположенной в два ряда напрягаемой арматуры Р = 480 кН; поперечная сила, постоянная по длине элемента, Q = 17 кН; максимальный изгибающий момент в сечении у конца элемента M_max = 23,8 кН•м; характеристики приведенного сечения: A_red = 58100 мм² , I_red = 286,7 • 10⁶ мм⁴ .

Требуется определить диаметр и шаг поперечных стержней (хомутов).

Р а с ч е т. h₀ = h - a = 240 - 40 = 200 мм.

Согласно п. 3.54, определим коэффициент j _n . Поскольку напрягаемая арматура расположена в два ряда и симметрично относительно центра тяжести сечения, в значении P учитываем усилие только от половины напрягаемой арматуры, т.е. Р = 0,5 • 480 = 240 кН.

Так как Р = 240 кН < N = 400 кН, j _n определяем по формуле (149):

= - 0.661 .

Поскольку ½j _n ½ = 0,661 < 0,8, оставляем j _n = - 0,661.

Согласно п. 3.19, выясним, требуются ли хомуты из условия прочности. Для этого проверим условие (93) при длине проекции наклонного сечения с, равной длине участка, где образуются нормальные трещины, т.е. при с = , где M_crc1  — внешний изгибающий момент, соответствующий образованию трещин.

Определим момент М_crc1 из условия (190), представив его в виде равенства

М_r = М_crc1 + Nr = М_crc = R_bt W_pl + Р (e_0p + r),

откуда при e_0p = 0 имеем

M_crc1 = R_bt W_pl + (P - N)r (здесь Р - полное усилие обжатая).

Согласно пп. 4.2 и 4.3, определяем W_pl и r:

= 120 мм ; = 239 × 10⁶ мм³ ;

W_pl = g W_red = 1,75 • 239 • 10⁶ = 4,18 • 10⁶ мм³ (здесь у = 1,75; см. табл. 39).

Принимая в целях упрощения расчета j = 0,8, имеем

= 32,9 мм .

Следовательно, М_crc1 = 1,1 • 4,18 • 10⁶ + (480 - 400) 10³ • 32,9 =
= 7,23 • 10⁶ H × мм = 7,23 кН × м;

= 0 ,975 м .

Поскольку с = 975 мм > 2,5 h ₀ = 2,5 • 200 = 500 мм, согласно п. 3.30,

Q_b1 = Q_b.min = j _b3 (1+ j _n )R_bt bh₀ = 0,6( - 0,661)1,1 × 220 × 200 =9845 H =95 кН,

где j _b3 = 0,6 (см. табл. 29).

Q_b1 = 9,85 кН < Q = 17 кН, т.е. условие (94) не выполняется, и хомуты подбираем из расчета по прочности согласно п. 3.23а.

По формуле (73) определяем М_b , принимая j _b2 = 2 (см. табл. 29) и j _f = 0:

M_b = j _b2 (1+ j _n ) R_bt bh₀ ² = 2(1 - 0,661)1,1 × 220 × 200² = 6,56 × 10⁶ H × мм.

Поскольку поперечная сила не изменяется по длине элемента, принимаем длину проекции с равной длине элемента, т.е. с = 2,8 м.

Q_b = M_b /с = 6,56/2,8 = 2,34 кН < Q_b,min = 9,85 кН.

Принимаем Q_b = Q_{b, min} = 9,85 кН.

Поскольку с = 2,8 м > 2/h₀ = 2 • 0,2 = 0,4 м, то c_o = 2h₀ = 0,4 м.

Тогда = 1 .

Так как х = = 0,727 < x₀ , значение q_sw определяем по формуле (79) :

= 21,25 кН/м .

Максимально допустимый шаг хомутов, согласно п. 3.21, равен:

=

= 289 мм > = 40 мм .

Принимаем шаг хомутов s = 200мм < 2b = 440 мм (см. п. 5.38).

Тогда = 16,3 мм² .

Принимаем два хомута диаметром по 4 мм (А_sw = 21,1 мм² ).

Элементы, работающие на кручение с изгибом

3.55. Расчет элементов, работающих на кручение с изгибом, производится согласно пп. 3.82—3.92 «Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры». При этом напрягаемая арматура учитывается в расчете аналогично ненапрягаемой со своим расчетным сопротивлением без учета коэффициента g _s6 , а ссылки на другие разделы указанного Пособия заменяются ссылками на соответствующие разделы настоящего Пособия (определение x _R по п. 3.6, расчет нормальных сечений по пп. 3.22—3.30, определение значения M_u по п. 3.43).

РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
НА ВЫНОСЛИВОСТЬ

3.56. Расчет железобетонных конструкций на выносливость производится при воздействии многократно повторяющейся (подвижной или пульсирующей) нагрузки, вызывающей значительный перепад напряжений в бетоне или растянутой арматуре, если число повторений нагрузки за период эксплуатации здания или сооружения достаточно велико (порядка 10⁵ и более).

Таким нагрузкам подвергаются подкрановые балки, эстакады, шпалы, перекрытия под неуравновешенные машины (например, вентиляторы, центрифуги) и т. п.

Подкрановые балки при легком режиме работы кранов на выносливость не рассчитываются.

3.57 (3.48). Расчет на выносливость сечений, нормальных к продольной оси элементов, должен производиться из условий:

а) для сжатого бетона

s _b,max £ R_b , (150)

где s _b,max  — максимальное нормальное напряжение в сжатом бетоне;

R_b  — расчетное сопротивление бетона сжатию, принимаемое по табл. 13 при g _b2 = 1,0 и умноженное на коэффициент условий работы g _b1 , определяемый согласно п. 3.60;

б) для растянутой арматуры

s _s,max £ R_s , (151)

где s _s,max  — максимальное напряжение в растянутой арматуре, определяемое по формуле

s _s,max = a ' s _bs + s _sp , (152)

здесь a '  — коэффициент приведения арматуры к бетону, принимаемый по табл. 34;

s _bs  — напряжение в бетоне на уровне наиболее растянутого ряда арматуры;

s _sp  — принимается при коэффициенте g _sp < 1,0;

R_s  — расчетное сопротивление растянутой арматуры, умноженное на коэффициент условий работы g _b3 , а при наличии сварных соединений — также на коэффициент g _s4 , определяемое согласно п. 3.61.

Таблица 34

Напряжения s _b,max и s _bs определяются от действия внешних нагрузок и от усилия предварительного обжатия Р как для упругого тела (см. п. 1.21) по приведенному сечению, принятому согласно п. 3.58.

В зоне, проверяемой по сжатому бетону, при действии многократно повторяющейся нагрузки следует избегать возникновения растягивающих напряжении.

Сжатая арматура на выносливость не рассчитывается.

3.58. При расчете на выносливость приведенное сечение принимается следующим образом:

если в сечении не образуются нормальные трещины, т.е. если выполняется условие (182) при замене в нем значения R_bt,ser на R_bt (при учете g _b1 ) , приведенное сечение включает в себя полное сечение бетона, а также площадь сечения всей продольной арматуры, умноженной на коэффициент приведения a¢ , определяемый по табл. 34;

если в сечении образуются нормальные трещины, приведенное сечение включает в себя площадь сечения только сжатого бетона, а также площадь сечения всей продольной арматуры, умноженную на коэффициент a '.

В этом случае высота сжатой зоны х для изгибаемых элементов определяется из уравнения

, (153)

где e_np  — расстояние от нейтральной линии до точки приложения усилия P:

e_np = y' + е_0p - x ; (154)

здесь у' — расстояние от центра тяжести полного приведенного сечения до наиболее сжатой грани;

I_b  — момент инерции сжатой зоны бетона относительно нейтральной линии;

S_b , S_sp , S_s , S ¢ _sp , S ¢ _s  — соответственно статические моменты сжатой зоны бетона и сечений напрягаемой и ненапрягаемой арматуры S и S ¢ относительно нейтральной линии;

у_sp , у'_sp , y_s , y ¢ _s  — расстояния от нейтральной линии соответственно до центра тяжести сечений напрягаемой и ненапрягаемой арматуры S и S' (черт. 35).

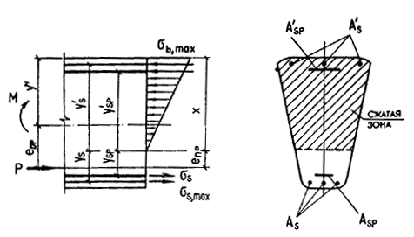
Черт. 35. Схема расположения усилий в поперечном сечении
с трещиной, рассчитываемом на выносливость

Для изгибаемых элементов, выполняемых без предварительного напряжения, уравнение (153) принимает вид

S_b - a 'S_s + a 'S'_s = 0. (155)

Для внецентренно сжатых или внецентренно растянутых элементов положение нейтральной линии также определяется из уравнения (153), левая часть которого принимается равной M_n / N_tot , гдеM_n  — момент внешней силы N и усилия обжатия Р относительно нейтральной линии; N_tot = Р ± N (знак «плюс» принимается при сжимающей силе N, знак «минус» — при растягивающей силе N).

Если точка приложения растягивающей силы N_tot (определенная с учетом всех внешних воздействий) находится между центрами тяжести арматуры S и S', в сечении возникают только растягивающие напряжения и в приведенном сечении учитывается только площадь сечения арматуры.

Для элементов прямоугольного, таврового или двутаврового сечений при наличии нормальных трещин уравнение (153) приобретает вид

; (156)

для изгибаемых элементов

e_s,tot = + e_sp ;

для внецентренно нагруженных элементов:

e_s,tot = ;

; ; .

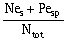Полученное из уравнения (156) значение x = x/h₀ должно удовлетворять условиям x ³ d и x £ (h - h_f ) / h₀ .

При отсутствии в сжатой зоне свесов в уравнении (156) принимается d _f = 2a ¢ / h₀ .

Для предварительно напряженных конструкций, у которых не образуются нормальные трещины, характеристики приведенного сечения допускается определять при коэффициенте приведения a = E_s / E_b .

3.59 (3.49). Расчет на выносливость сечений, наклонных к продольной оси элемента, должен производиться из условия, что равнодействующая главных растягивающих напряжений, действующих на уровне центра тяжести приведенного сечения, должна быть полностью воспринята поперечной арматурой при напряжениях в ней, равных сопротивлениям R_s , т.е. должно выполняться условие

, (157)

где s _mt - главное растягивающее напряжение на уровне центра тяжести приведенного сечения, вычисляемое согласно п. 4.9;

s _y , t _ху - соответственно сжимающее напряжение в направлении, перпендикулярном продольной оси, и касательное напряжение, определяемые на том же уровне, что и напряжение s _mt , согласно пп. 4.10-4.12;

R_s - расчетное сопротивление хомутов и отгибов с учетом коэффициентов условий работы g _s3 и g _s4 (см. п. 3.61);

q - угол наклона отгибов к продольной оси элемента на уровне центра тяжести сечения в рассматриваемом сечении;

s_inc - расстояние между плоскостями отгибов, измеренное по нормали к ним; при одной плоскости отгибов за s_inc принимается расстояние между этой плоскостью и гранью опоры; при двух и более плоскостях отгибов значение s_inc определяется согласно черт. 36.

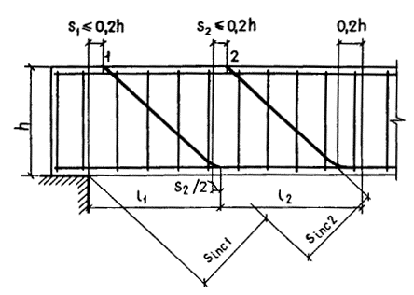
Черт. 36. Учет отогнутых стержней при расчете наклонных сечений
на выносливость

1-1, 2-2 - плоскости отгибов; для 1-1 s_inc = (s_inc1 + s_inc2 )/2; для 2-2 s_inc = s_inc2 ; l₁ и l₂ - длины участков элемента при учете соответственно плоскостей отгибов 1-1 и 2-2

Отгибы учитываются в расчете, если расстояние от грани опоры до начала первого отгиба (s₁ ), а также расстояние между концом предыдущего и началом следующего отгиба (s₂ ) не превышают 0,2h (см. черт. 36).

При вычислении s _mt , s _у и t _xy приведенное сечение определяется согласно п. 3.58.

Расчет производится для каждого участка с постоянной интенсивностью поперечного армирования. При наличии отгибов учитывается среднее значение s _mt на участке рассматриваемого отгиба (см. черт. 36).

Для элементов, в которых поперечная арматура не предусматривается (см. п. 5.41), должны быть выполнены требования п. 4.9 при замене в условиях (183) и (184) расчетных сопротивлений бетона R_b,ser и R_bt,ser соответственно расчетными сопротивлениями R_b и R_bt , умноженными на коэффициент условий работы g _b1 согласно табл. 35.

Таблица 35 (16)

• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6
• часть 7
• часть 8
• часть 9
• часть 10
• часть 11