СНиП II-23-81 (1990), часть 2
В составных стержнях с решетками помимо расчета на устойчивость стержня в целом следует проверять устойчивость отдельных ветвей на участках между узлами.
Гибкость отдельных ветвей l 1 , l 2 и l 3 на участке между планками должна быть не более 40.
При наличии в одной из плоскостей сплошного листа вместо планок (рис. 1, б , в ) гибкость ветви должна вычисляться по радиусу инерции полусечения относительно его оси, перпендикулярной плоскости планок.
В составных стержнях с решетками гибкость отдельных ветвей между узлами должна быть не более 80 и не должна превышать приведенную гибкость l ef стержня в целом. Допускается принимать более высокие значения гибкости ветвей, но не более 120, при условии, что расчет таких стержней выполнен по деформированной схеме.
5.7. Расчет составных элементов из уголков, швеллеров и т. п., соединенных вплотную или через прокладки, следует выполнять как сплошностенчатых при условии, что наибольшие расстояния на участках между приваренными планками (в свету) или между центрами крайних болтов не превышают:
для сжатых элементов 40i
для растянутых элементов 80i
Здесь радиус инерции i уголка или швеллера следует принимать для тавровых или двутавровых сечений относительно оси, параллельной плоскости расположения прокладок, а для крестовых сечений – минимальный.
При этом в пределах длины сжатого элемента следует ставить не менее двух прокладок.
5.8*. Расчет соединительных элементов (планок, решеток) сжатых составных стержней должен выполняться на условную поперечную силу Qfic , принимаемую постоянной по всей длине стержня и определяемую по формуле
Qfic = 7,15 × 10-6 (2330– E /Ry )N /j , (23)*
где N – продольное усилие в составном стержне;
j – коэффициент продольного изгиба, принимаемый для составного стержня в плоскости соединительных элементов.
Условную поперечную силу Qfic следует распределять:
при наличии только соединительных планок (решеток) поровну между планками (решетками), лежащими в плоскостях, перпендикулярных оси, относительно которой производится проверка устойчивости;
при наличии сплошного листа и соединительных планок (решеток) – пополам между листом и планками (решетками), лежащими в плоскостях, параллельных листу;
при расчете равносторонних трехгранных составных стержней условная поперечная сила, приходящаяся на систему соединительных элементов, расположенных в одной плоскости, должна приниматься равной 0,8Qfic .

5.9. Расчет соединительных планок и их прикрепления (рис. 3) должен выполняться как расчет элементов безраскосных ферм на:
силу F , срезывающую планку, по формуле
F = Qs l /b ; (24)
момент M1 , изгибающий планку в ее плоскости, по формуле
M1 = Qs l /2 (25)
где Qs – условная поперечная сила, приходящаяся на планку одной грани.

5.10. Расчет соединительных решеток должен выполняться как расчет решеток ферм. При расчете перекрестных раскосов крестовой решетки с распорками (рис. 4) следует учитывать дополнительное усилие Nad , возникающее в каждом раскосе от обжатия поясов и определяемое по формуле
![]() (26)
(26)
где N – усилие в одной ветви стержня;
А – площадь сечения одной ветви;
Ad – площадь сечения одного раскоса;
a – коэффициент, определяемый по формуле
a = a l 2 /(a 3 =2b 3 ) (27)
где a , l и b – размеры, указанные на рис. 4.

5.11. Расчет стержней, предназначенных для уменьшения расчетной длины сжатых элементов, должен выполняться на усилие, равное условной поперечной силе в основном сжатом элементе, определяемой по формуле (23)*.
ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ
5.12. Расчет на прочность элементов (кроме балок с гибкой стенкой, с перфорированной стенкой и подкрановых балок), изгибаемых в одной из главных плоскостей, следует выполнять по формуле
![]() (28)
(28)
Значение касательных напряжений t в сечениях изгибаемых элементов должны удовлетворять условию
![]() (29)
(29)
При наличии ослабления стенки отверстиями для болтов значения t в формуле (29) следует умножать на коэффициент a , определяемый по формуле
a = a /(a – d ), (30)
где a – шаг отверстий;
b – диаметр отверстия.
5.13. Для расчета на прочность стенки балки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балки, не укрепленных ребрами жесткости, следует определять местное напряжение s loc по формуле
![]() (31)
(31)
где F – расчетное значение нагрузки (силы);
lef – условная длина распределения нагрузки, определяемая в зависимости от условий опирания; для случая опирания по рис. 5.
lef = b + 2tf , (32)
где tf – толщина верхнего пояса балки, если нижняя балка сварная (рис. 5, а ), или расстояние от наружной грани полки до начала внутреннего закругления стенки, если нижняя балка прокатная (рис. 5, б ).

5.14*. Для стенок балок, рассчитываемых по формуле (28), должны выполняться условия:
![]() (33)
(33)
где
![]() –
нормальные
напряжения в срединной плоскости стенки, параллельные оси балки;
–
нормальные
напряжения в срединной плоскости стенки, параллельные оси балки;
s y – то же, перпендикулярные оси балки, в том числе s loc , определяемое по формуле (31);
t x y – касательное напряжение, вычисляемое по формуле (29) с учетом формулы (30).
Напряжения s x и s y , принимаемые в формуле (33) со своими знаками, а также t xy следует определять в одной и той же точке балки.
5.15. Расчет на устойчивость балок двутаврового сечения, изгибаемых в плоскости стенки и удовлетворяющих требованиям пп. 5.12 и 5.14*, следует выполнять по формуле
![]() (34)
(34)
где Wc – следует определять для сжатого пояса;
j b – коэффициент, определяемый по прил. 7*.
При определении значения j b за расчетную длину балки lef следует принимать расстояние между точками закреплений сжатого пояса от поперечных смещений (узлами продольных или поперечных связей, точками крепления жесткого настила); при отсутствии связей lef = l (где l – пролет балки) за расчетную длину консоли следует принимать: lef = l при отсутствии закрепления сжатого пояса на конце консоли в горизонтальной плоскости (здесь l – длина консоли); расстояние между точками закреплений сжатого пояса в горизонтальной плоскости при закреплении пояса на конце и по длине консоли.
5.16*. Устойчивость балок не требуется проверять:
а) при передаче нагрузки через сплошной жесткий настил, непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (плиты железобетонные из тяжелого, легкого и ячеистого бетона, плоский и профилированный металлический настил, волнистую сталь и т. п.);
б) при отношении расчетной длины балки lef к ширине сжатого пояса b , не превышающем значений, определяемых по формулам табл. 8* для балок симметричного двутаврового сечения и с более развитым сжатым поясом, для которых ширина растянутого пояса составляет не менее 0,75 ширины сжатого пояса.
Таблица 8*
|
Место приложения нагрузки |
Наибольшие значения lef /b , при которых не требуется расчет на устойчивость прокатных и сварных балок (при 1 £ h /b < 6 и 15 £ b /t £ 35) |
|
К верхнему поясу |
|
|
К нижнему поясу |
|
|
Независимо от уровня приложения нагрузки при расчете участка балки между связями или при чистом изгибе |
|
|
Обозначения, принятые в таблице 8*: b и t – соответственно ширина и толщина сжатого пояса; h – расстояние (высота) между осями поясных листов. Примечания: 1. Для балок с поясными соединениями на высокопрочных болтах значения lef /b , получаемые по формулам таблицы 8* следует умножать на коэффициент 1,2. 2. Для балок с отношением b /t < 15 в формулах таблицы 8* следует принимать b /t = 15. |
|
Закрепление сжатого пояса в горизонтальной плоскости должно быть рассчитано на фактическую или условную поперечную силу. При этом условную поперечную силу следует определять:
при закреплении в отдельных точках по формуле (23)*, в которой j следует определять при гибкости l = lef /i (здесь i – радиус инерции сечения сжатого пояса в горизонтальной плоскости), а N следует вычислять по формуле
N = (Af + 0,25AW )Ry ; (37, а)
при непрерывном закреплении по формуле
qfic = 3Qfic /l , (37, б)
где qfic – условная поперечная сила на единицу длины пояса балки;
Qfic – условная поперечная сила, определяемая по формуле (23)*, в которой следует принимать j = 1, а N – определять по формуле (37,а).
5.17. Расчет на прочность элементов, изгибаемых в двух главных плоскостях, следует выполнять по формуле
![]() (38)
(38)
где x и y – координаты рассматриваемой точки сечения относительно главных осей.
В балках, рассчитываемых по формуле (38), значения напряжений в стенке балки должны быть проверены по формулам (29) и (33) в двух главных плоскостях изгиба.
При выполнении требований п. 5.16*, а проверка устойчивости балок, изгибаемых в двух плоскостях, не требуется.
5.18*. Расчет на прочность разрезных балок сплошного сечения из стали с пределом текучести до 530 МПа (5400 кгс/см2 ), несущих статическую нагрузку, при соблюдении пп. 5.19*– 5.21, 7.5 и 7.24 следует выполнять с учетом развития пластических деформаций по формулам
при изгибе в одной из главных плоскостей при касательных напряжениях t £ 0,9Rs (кроме опорных сечений)
![]() (39)
(39)
при изгибе в двух главных плоскостях при касательных напряжениях t £ 0,5Rs (кроме опорных сечений)
 (40)
(40)
здесь M , Mx и My – абсолютные значения изгибающих моментов;
c1 – коэффициент, определяемый по формулам (42) и (43);
cx и cy – коэффициенты, принимаемые по табл. 66.
Расчет в опорном сечении балок (при M = 0; Mx = 0 и My = 0) следует выполнять по формуле
![]() (41)
(41)
При наличии зоны чистого изгиба в формулах (39) и (40) вместо коэффициентов c1 , cx и су следует принимать соответственно:
c1m = 0,5(1+c ); cxm = 0,5(1+cx ); сym = 0,5(1+cy ).
При одновременном действии в сечении момента М и поперечной силы Q коэффициент с1 следует определять по формулам:
при t £ 0,5Rs c 1 = c ; (42)
при 0,5Rs < t £ 0,9Rs c1 = 1,05b c , (43)
где
 (44)
(44)
здесь с – коэффициент, принимаемый по табл. 66;
t и h – соответственно толщина и высота стенки;
a – коэффициент, равный a = 0,7 для двутаврового сечения, изгибаемого в плоскости стенки; a = 0 – для других типов сечений;
с1 – коэффициент, принимаемый не менее единицы и не более коэффициента с .
С целью оптимизации балок при их расчете с учетом требований пп. 5.20, 7.5, 7.24 и 13.1 значения коэффициентов с , сх и су в формулах (39) и (40) допускается принимать меньше значений, приведенных в табл. 66, но не менее 1,0.
При наличии ослабления стенки отверстиями для болтов значения касательных напряжений t следует умножать на коэффициент, определяемый по формуле (30).
5.19*. Расчет на прочность балок переменного сечения с учетом развития пластических деформаций следует выполнять только для одного сечения с наиболее неблагоприятным сочетанием усилий M и Q ; в остальных сечениях учитывать развитие пластических деформаций не допускается.
Расчет на прочность изгибаемых элементов из стали с пределом текучести до 530 МПа (5400 кгс/см2 ), воспринимающих динамические, вибрационные или подвижные нагрузки, допускается выполнять с учетом развития пластических деформаций, не препятствующих требуемым условиям эксплуатации конструкций и оборудования.
5.20. Для обеспечения общей устойчивости балок, рассчитываемых с учетом развития пластических деформаций, необходимо, чтобы либо были выполнены требования п. 5.16*,а, либо наибольшие значения отношений расчетной длины балки к ширине сжатого пояса lef /b , определяемые по формулам табл. 8*, были уменьшены умножением на коэффициент
d = [1 – 0,7(c1 – 1)/(c – 1)], здесь 1 < c1 £ c .
Учет пластичности при расчете балок со сжатым поясом менее развитым, чем растянутый, допускается лишь при выполнении условий п. 5.16*,а.
5.21. В балках, рассчитываемых с учетом развития пластических деформаций, стенки следует укреплять поперечными ребрами жесткости согласно требованиям пп. 7.10, 7.12 и 7.13, в том числе в местах приложения сосредоточенной нагрузки.
5.22. Расчет на прочность неразрезных и защемленных балок постоянного двутаврового сечения, изгибаемых в плоскости наибольшей жесткости, со смежными пролетами, отличающимися не более чем на 20 %, несущих статическую нагрузку, при условии соблюдения требований пп. 5.20, 5.21, 7.5 и 7.24 следует выполнять по формуле (39) с учетом перераспределения опорных и пролетных моментов.
Расчетные значения изгибающего момента М следует определять по формуле
М = a Mmax , (45)
где Mmax – наибольший изгибающий момент в пролете или на опоре, определяемый из расчета неразрезной балки в предположении упругой работы материала;
a – коэффициент перераспределения моментов, определяемый по формуле
 (46)
(46)
здесь Mef – условный изгибающий момент, равный:
а) в неразрезных балках со свободно опертыми концами большему из значений
![]() (47)
(47)
Mef = 0,5M 2 , (48)
где символ max означает, что следует найти максимум всего следующего за ним выражения;
M 1 – изгибающий момент в крайнем пролете, вычисленный как в свободно опертой однопролетной балке;
М 2 – максимальный изгибающий момент в промежуточном пролете, вычисленный как в свободно опертой однопролетной балке;
а – расстояние от сечения, в котором действует момент М 1 , до крайней опоры;
l – длина крайнего пролета;
б) в однопролетных и неразрезных балках с защемленными концами Mef = 0,5М 3 , где М 3 – наибольший из моментов, вычисленных как в балках с шарнирами на опорах;
в) в балке с одним защемленным и другим свободно опертым концом значение Mef следует определять по формуле (47).
Расчетное значение поперечной силы Q в формуле (44) следует принимать в месте действия Mmax . Если Mmax – момент в пролете, следует проверить опорное сечение балки.
5.23. Расчет на прочность неразрезных и защемленных балок, удовлетворяющих требованиям п. 5.22, в случае изгиба в двух главных плоскостях при t £ 0,5Rs следует производить по формуле (40) с учетом перераспределения опорных и пролетных моментов в двух главных плоскостях согласно требованиям п. 5.22.
ЭЛЕМЕНТЫ, ПОДВЕРЖЕННЫЕ ДЕЙСТВИЮ ОСЕВОЙ СИЛЫ С ИЗГИБОМ
5.24*. Расчет на прочность внецентренно-сжатых и сжато-изгибаемых элементов по формуле (49) выполнять не требуется при значении приведенного эксцентриситета mef £ 20, отсутствии ослабления сечения и одинаковых значениях изгибающих моментов, принимаемых в расчетах на прочность и устойчивость.
5.25*. Расчет на прочность внецентренно-сжатых, сжато-изгибаемых, внецентренно-растянутых и растянуто-изгибаемых элементов из стали с пределом текучести до 530 МПа (5400 кгс/см2 ), не подвергающихся непосредственному воздействию динамических нагрузок, при t £ 0,5Rs и N /(An Ry ) > 0,1 следует выполнять по формуле
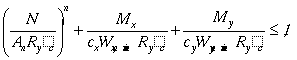 (49)
(49)
где N , Mx и My – абсолютные значения соответственно продольной силы и изгибающих моментов при наиболее неблагоприятном их сочетании;
n , cx и cy – коэффициенты, принимаемые по прил. 5.
Если N /(An Ry ) £ 0,1, формулу (49) следует применять при выполнении требований пп. 7.5 и 7.24.
В прочих случаях расчет следует выполнять по формуле
![]() (50)
(50)
где х и у – координаты рассматриваемой точки сечения относительно его главных осей.
5.26. Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых элементов следует выполнять как в плоскости действия момента (плоская форма потери устойчивости), так и из плоскости действия момента (изгибно-крутильная форма потери устойчивости).
5.27*. Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых элементов постоянного сечения (с учетом требований пп. 5.28* и 5.33 настоящих норм) в плоскости действия момента, совпадающей с плоскостью симметрии, следует выполнять по формуле
![]() (51)
(51)
В формуле (51) коэффициент j e следует определять:
а) для сплошностенчатых стержней по
табл. 74 в зависимости от условной гибкости
![]() и приведенного относительного эксцентриситета mef
,
определяемого по формуле
и приведенного относительного эксцентриситета mef
,
определяемого по формуле
mef = h m , (52)
где h – коэффициент влияния формы сечения, определяемый по табл. 73;
![]() – относительный эксцентриситет (здесь е
–
эксцентриситет;
– относительный эксцентриситет (здесь е
–
эксцентриситет;
Wc – момент сопротивления сечения для наиболее сжатого волокна);
б) для сквозных стержней с решетками
или планками, расположенными в плоскостях, параллельных плоскости
изгиба, по табл. 75 в зависимости от условной приведенной гибкости
![]() ef
(l
ef
по табл. 7)
и относительного эксцентриситета m
, определяемого по формуле
ef
(l
ef
по табл. 7)
и относительного эксцентриситета m
, определяемого по формуле
![]() (53)
(53)
где а – расстояние от главной оси сечения, перпендикулярной плоскости изгиба, до оси наиболее сжатой ветви, но не менее расстояния до оси стенки ветви.
При вычислении эксцентриситета e = M /N значения M и N следует принимать согласно требованиям п. 5.29.
Расчет на устойчивость внецентренно-сжатых и сжато-изгибаемых трехгранных сквозных стержней с решетками или планками и постоянным по длине равносторонним сечением следует выполнять согласно требованиям разд. 15*.
Расчет на устойчивость не требуется для сплошно-стенчатых стержней при mef > 20 и для сквозных стержней при m > 20, в этих случаях расчет следует выполнять как для изгибаемых элементов.
5.28*. Внецентренно-сжатые элементы, выполненные из стали с пределом текучести свыше 530 МПа (5400 кгс/см2 ) и имеющие резко несимметричные сечения (типы сечений 10 и 11 по табл. 73), кроме расчета по формуле (51), должны быть проверены на прочность по формуле
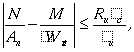 (54)
(54)
где значение Wnt следует вычислять для растянутого волокна, а коэффициент d определять по формуле
d = 1 – Nl 2 /(p 2 EA ). (55)
5.29. Расчетные значения продольной силы N и изгибающего момента М в элементе следует принимать для одного и того же сочетания нагрузок из расчета системы по недеформированной схеме в предположении упругих деформаций стали.
При этом значения М следует принимать равными:
для колонн постоянного сечения рамных систем – наибольшему моменту в пределах длины колонн;
для ступенчатых колонн – наибольшему моменту на длине участка постоянного сечения;
для колонн с одним защемленным, а другим свободным концом – моменту в заделке, но не менее момента в сечении, отстоящем на треть длины колонны от заделки;
для сжатых верхних поясов ферм и структурных плит, воспринимающих внеузловую нагрузку, – наибольшему моменту в пределах средней трети длины панели пояса, определяемому из расчета пояса как упругой неразрезной балки;
для сжатых стержней с шарнирно-опертыми концами и сечениями, имеющими одну ось симметрии, совпадающую с плоскостью изгиба, – моменту, определяемому по формулам табл. 9.
Таблица 9
|
Относительный эксцентриситет, |
Расчетные значения M при условной гибкости стержня |
|
|
соответствующий Mmax |
|
|
|
m £ 3 |
|
M = M 1 |
|
3 < m £ 20 |
|
|
|
Обозначения, принятые в таблице 9: Mmax – наибольший изгибающий момент в пределах длины стержня; M 1 – наибольший изгибающий момент в пределах средней трети длины стержня, но не менее 0,5Mmax ; m – относительный эксцентриситет, определяемый по формуле m = Mmax A /(NWc ). Примечание. Во всех случаях следует принимать M ³ 0,5Mmax . |
||
Для сжатых стержней с шарнирно-опертыми концами и сечениями, имеющими две оси симметрии, расчетные значения эксцентриситетов mef следует определять по табл. 76.
5.30. Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения из плоскости действия момента при изгибе их в плоскости наибольшей жесткости (Jx > Jy ), совпадающей с плоскостью симметрии, следует выполнять по формуле
![]() (56)
(56)
где с – коэффициент, вычисляемый согласно требованиям п. 5.31;
j y – коэффициент, вычисляемый согласно требованиям п. 5.3 настоящих норм.
5.31. Коэффициент с в формуле (56) следует определять:
при значениях относительного эксцентриситета mx £ 5 по формуле
![]() (57)
(57)
где a и b – коэффициенты, принимаемые по табл. 10;
Таблица 10
|
|
Значения коэффициентов |
||||
|
Типы сечений |
a при |
b при |
|||
|
|
mx £ 1 |
1 < mx £ 5 |
l y £ l c |
l y > l c |
|
|
Открытые
|
0,7 |
0,65 + 0,05mx |
1 |
|
|
|
|
|
|
1 |
при J 2 /J 1 < 0,5 b = 1 |
|
|
Замкнутые: |
|
|
|
|
|
|
с решетками (с планками) |
сплошные |
|
|
|
|
|
|
|
0,6 |
0,55 + 0,05mx |
1 |
|
Обозначения, принятые в таблице 10:
J 1 и J 2 – моменты инерции соответственно большей и меньшей полок относительно оси симметрии сечения y – y ;
j
c
–
значенияj
y
при![]()
Примечание. Значения коэффициентов a и b для сквозных стержней с решетками (или планками) следует принимать как для замкнутых сечений при наличии не менее двух промежуточных диафрагм по длине стержня. В противном случае следует принимать коэффициенты, установленные для стержней открытого двутаврового сечения.
при значениях относительного эксцентриситета mx ³ 10 по формуле
![]() (58)
(58)
где j b – коэффициент, определяемый согласно требованиям п. 5.15 и прил. 7* как для балки с двумя и более закреплениями сжатого пояса; для замкнутых сечений j b = 1,0;
при значениях относительного эксцентриситета 5 < mx < 10 по формуле
c = c 5 (2 – 0,2mx ) + с 10 (0,2mx – 1), (59)
где с 5 определяется по формуле (57) при mx = 5, a c 10 – по формуле (58) при mx = 10.
При определении относительного эксцентриситета mx за расчетный момент Mx следует принимать:
для стержней с шарнирно-опертыми концами, закрепленными от смещения перпендикулярно плоскости действия момента, – максимальный момент в пределах средней трети длины (но не менее половины наибольшего по длине стержня момента);
для стержней с одним защемленным, а другим свободным концом – момент в заделке (но не менее момента в сечении, отстоящем на треть длины стержня от заделки).
При гибкости
![]() коэффициент с
не должен превышать:
коэффициент с
не должен превышать:
для стержней замкнутого сечения – единицы;
для стержней двутаврового сечения с двумя осями симметрии – значений, определяемых по формуле
 (60)
(60)
где
d
= 4r
/m
;
r
= (Jx
+
Jy
)/(Ah
2
);
![]() ;
Jt
= 0,433S
bi
ti
3
;
;
Jt
= 0,433S
bi
ti
3
;
здесь bi и ti – соответственно ширина и толщина листов, образующих сечение;
h – расстояние между осями поясов;
для двутавровых и тавровых сечений с одной осью симметрии коэффициенты с не должны превышать значений, определяемых по формуле (173) прил. 6.
5.32. Внецентренно-сжатые элементы, изгибаемые в плоскости наименьшей жесткости (Jy < Jx и ey ¹ 0), при l x > l y следует рассчитывать по формуле (51), а также проверять на устойчивость из плоскости действия момента как центрально-сжатые стержни по формуле
![]() ,
(61)
,
(61)
где j x – коэффициент, принимаемый согласно требованиям п. 5.3 настоящих норм.
При l x £ l y проверка устойчивости из плоскости действия момента не требуется.
5.33. В сквозных внецентренно-сжатых стержнях с решетками, расположенными в плоскостях, параллельных плоскости изгиба, кроме расчета на устойчивость стержня в целом по формуле (51) должны быть проверены отдельные ветви как центрально-сжатые стержни по формуле (7).
Продольную силу в каждой ветви следует определять с учетом дополнительного усилия от момента. Значение этого усилия при изгибе в плоскости, перпендикулярной оси y – y (табл. 7), должно быть определено по формулам: Nad = M /b – для сечений типов 1 и 3; Nad = M /2d – для сечения типа 2; для сечения типа 3 при изгибе в плоскости, перпендикулярной оси х – х , усилие от момента Nad = 1,16M /b (здесь b – расстояние между осями ветвей).
Отдельные ветви внецентренно-сжатых сквозных стержней с планками следует проверять на устойчивость как внецентренно-сжатые элементы с учетом усилий от момента и местного изгиба ветвей от фактической или условной поперечной силы (как в поясах безраскосной фермы), а также п. 5.36 настоящих норм.
5.34. Расчет на устойчивость сплошностенчатых стержней, подверженных сжатию и изгибу в двух главных плоскостях, при совпадении плоскости наибольшей жесткости (Jx > Jy ) с плоскостью симметрии следует выполнять по формуле
![]() ,
(62)
,
(62)
где
![]()
здесь j ey следует определять согласно требованиям п. 5.27* с заменой в формулах m и l соответственно на my и l y , а c – согласно требованиям п. 5.41.
При вычислении приведенного относительного эксцентриситета mef,y = h my для стержней двутаврового сечения с неодинаковыми полками коэффициент h следует определять как для сечения типа 8 по табл. 73.
Если mef,y < mx то кроме расчета по формуле (62) следует произвести дополнительную проверку по формулам (51) и (56), принимая ey = 0.
Значения относительных эксцентриситетов следует определять по формулам:
![]() и
и
![]() ,
(63)
,
(63)
где Wcx и Wcy – моменты сопротивления сечений для наиболее сжатого волокна относительно осей соответственно х – х и у – у .
Если l x > l y , то кроме расчета по формуле (62) следует произвести дополнительную проверку по формуле (51), принимая ey = 0
В случае несовпадения плоскости наибольшей жесткости (Jx > Jy ) с плоскостью симметрии расчетное значение mx следует увеличить на 25%.

5.35. Расчет на устойчивость сквозных стержней из двух сплошностенчатых ветвей, симметричных относительно оси у – у (рис. 6), с решетками в двух параллельных плоскостях, подверженных сжатию и изгибу в обеих главных плоскостях, следует выполнять:
для стержня в целом – в плоскости, параллельной плоскостям решеток, согласно требованиям п. 5.27*, принимая ey = 0;
для отдельных ветвей – как внецентренно-сжатых элементов по формулам (51) и (56), при этом продольную силу в каждой ветви следует определять с учетом усилия от момента Mx (см. п. 5.33), а момент My распределять между ветвями пропорционально их жесткостям (если момент Му действует в плоскости одной из ветвей, то следует считать его полностью передающимся на эту ветвь). Гибкость отдельной ветви следует определять при расчете по формуле (51) согласно требования п. 6.13 настоящих норм, при расчете по формуле (56) – по максимальному расстоянию между узлами решетки.
5.36. Расчет соединительных планок или решеток сквозных внецентренно-сжатых стержней следует выполнять согласно требованиям п. 5.9 и 5.10 настоящих норм на поперечную силу, равную большему из двух значений: фактическую поперечную силу Q или условную поперечную силу Qfic , вычисляемую согласно требованиям п. 5.8* настоящих норм.
В случае, когда фактическая поперечная сила больше условной, соединять планками ветви сквозных внецентренно-сжатых элементов, как правило, не следует.
ОПОРНЫЕ ЧАСТИ
5.37. Неподвижные шарнирные опоры с центрирующими прокладками, тангенциальные, а при весьма больших реакциях – балансирные опоры следует применять при необходимости строго равномерного распределения давления под опорой.
Плоские или катковые подвижные опоры следует применять в случаях, когда нижележащая конструкция должна быть разгружена от горизонтальных усилий, возникающих при неподвижном опирании балки или фермы.
Коэффициент трения в плоских подвижных опорах принимается равным 0,3, в катковых – 0,03.
5.38. Расчет на смятие в цилиндрических шарнирах (цапфах) балансирных опор следует выполнять (при центральном угле касания поверхностей, равном или большем p / 2) по формуле
![]() ,
(64)
,
(64)
где F – давление (сила) на опору;
r и l – соответственно радиус и длина шарнира;
Rlp – расчетное сопротивление местному смятию при плотном касании, принимаемое согласно требованиям п. 3.1* настоящих норм.
5.39. Расчет на диаметральное сжатие катков должен производиться по формуле
![]() (65)
(65)
где n – число катков;
d и l – соответственно диаметр и длина катка;
Rcd – расчетное сопротивление диаметральному сжатию катков при свободном касании, принимаемое согласно требованиям п. 3.1.* настоящих норм.
6. РАСЧЕТНЫЕ ДЛИНЫ И ПРЕДЕЛЬНЫЕ ГИБКОСТИ ЭЛЕМЕНТОВ СТАЛЬНЫХ КОНСТРУКЦИЙ
РАСЧЕТНЫЕ ДЛИНЫ ЭЛЕМЕНТОВ ПЛОСКИХ ФЕРМ И СВЯЗЕЙ
6.1. Расчетные длины lef элементов плоских ферм и связей, за исключением элементов перекрестной решетки ферм, следует принимать по табл. 11.
Таблица 11
|
Направление |
Расчетная длина lef |
||
|
продольного изгиба |
поясов |
опорных раскосов и опорных стоек |
прочих элементов решетки |
|
1. В плоскости фермы: |
|
|
|
|
а) для ферм, кроме указанных в поз. 1, б |
l |
l |
0,8l |
|
б) для ферм из одиночных уголков и ферм с прикреплением элементов решетки к поясам впритык |
l |
l |
0,9l |
|
2. В направлении, перпендикулярном плоскости фермы (из плоскости фермы): |
|
|
|
|
а) для ферм, кроме указанных в поз. 2, б |
l 1 |
l 1 |
l 1 |
|
б) для ферм с поясами из замкнутых профилей с прикреплением элементов решетки к поясам впритык |
l 1 |
l 1 |
0,9l 1 |
|
Обозначения, принятые в табл. 11 (рис. 7): l – геометрическая длина элемента (расстояние между центрами узлов) в плоскости фермы; l 1 – расстояние между узлами, закрепленными от смещения из плоскости фермы (поясами ферм, специальными связями, жесткими плитами покрытий, прикрепленными к поясу сварными швами или болтами, и т. п. |
|||

6.2. Расчетную длину lef элемента, по длине которого действуют сжимающие силы N 1 и N 2 (N 1 > N 2 ), из плоскости фермы (рис. 7, в , г ; рис. 8) следует вычислять по формуле
 (66)
(66)
Расчет на устойчивость в этом случае следует выполнять на силу N 1 .

6.3*. Расчетные длины lef элементов перекрестной решетки, скрепленных между собой (рис. 7, д ), следует принимать:
в плоскости фермы – равными расстоянию от центра узла фермы до точки их пересечения (lef = 1);

 (35)
(35) (36)
(36) (37)
(37)