Проект. асбестоцем. констр. (к СНиП 2.03.09-85), часть 3
(25·
10-2
·
10-6
/12)
+
+ (4,18· 10-2 – 0,5· 10-2 )2 · 25· 10-4 = 341· 10-8 м4 ;
582,7·
10-8
+
+ (8· 10-2 – 4,18· 10-2 )2 · 23,76· 10-4 = 929,4· 10-8 м4 .
По формуле [16] находим приведенный момент инерции сечения конструкции
= 929,4· 10-8 + 0,892 (0,1· 105 /0,09· 105 )341· 10-8 = 1266,6· 10-8 м4 .
Статический момент сдвигаемой части поперечного сечения относительно нейтральной оси:
= 5,7·
10-4
(10,82·
10-2
– 0,7·
10-2
)
+
+ 10,3· 10-4 · 4,71· 10-2 = 106,1· 10-6 м3 .
Б. Определение геометрических характеристик среднего ребра и прилегающей к нему части обшивки
Положение
нейтральной оси и геометрические характеристики среднего ребра и
прилегающей к нему обшивки определяются так же, как и для крайнего
участка плиты; при этом в соответствии с [п. 4.3]
расчетом учитываем часть площади поперечного сечения обшивки шириной
b
= 25
= 25·
10-2
= 025 м в каждую сторону от вертикальной оси ребра.
Сравнение геометрических характеристик крайних и среднего участков плиты показывает, что они отличаются в два раза. Нагрузка, которая воспринимается этими участками, также отличается в два раза, поэтому дальнейший расчет производится только для крайних участков.
Определение напряжений в каркасе и обшивке
Напряжения в элементах
плиты определяются по формулам [12] – [15]. По формуле [19]
определяем коэффициент
=0,47
Напряжения в обшивке:
=
2,62
МПа.
Напряжения в каркасе (швеллере):
= 1,84 МПа;
МПа.
Касательные напряжения в каркасе плиты:
МПа.
Напряжения в клеевом соединении обшивки с каркасом определяем по формуле [ 15] :
МПа.
Проверка прочности элементов плиты
Проверка прочности элементов плиты покрытия проводится по формулам [1], [3], [4], [8].
В
соответствии с п. 3.2 расчетные сопротивления экструзионного и
листового асбестоцемента умножаются на коэффициенты условий работы
и
.
Для
определения
находим значения
.
Определяя изгибающий момент от постоянной нагрузки, получим
=
234 Н·
м.
Рассчитываем напряжения от постоянной нагрузки в обшивке:
=
0
,5(1 – 0,47)234·
4,18·
10-2
·
0,1·
105
/0,89·
0,1·
1
05
·
341·
10-8
= 0,84 МПа.
Отсюда
.
По
[п.3.2б]
находим коэффициент=
0,9.
Проведя проверку прочности плиты, получим:
=
2,62 МПа <
= 6·
0,9·
0,76
= 4,10 МПа;
=
6,2 МПа <
=
11·
0,9·
0,76
= 7,52 МПа;
=
1,84 МПа <
= 11·
0,9·
0,76
= 7,52 МПа;
=
0,75 МПа <
=
3,2·
0,9·
0,76
= 2,19 МПа;
= 0,39 МПа <
=
2,5 МПа.
Расчет и проверка прогибов плиты
Прогиб определяем по формуле
м.
В соответствии с [п. 4.24] прогиб плит не должен превышать 1/200 пролета.
Проведя проверку прогибов, получим:
f = 0,43· 10-2 <f пред = ll /200 = 1· 3/200 = 1,5· 10-2 м.
Находим прогиб плиты от постоянной и временной длительной нагрузки. Согласно СНиП 2.01.07–85 для II снегового района вся снеговая нагрузка принимается кратковременной
.
По
[п. 3.4] коэффициент условий работы для модуля упругости
=
0,65:
м.
Проведя проверку прогибов, получим
f = 0,29· 10-2 < f пред = 1,5· 10-2 м.
ПРИМЕР 5. РАСЧЕТ СТЕНОВОЙ ПАНЕЛИ С МЕТАЛЛИЧЕСКИМ КАРКАСОМ
В качестве примера рассмотрим расчет на прочность стеновой панели на алюминиевом каркасе с асбестоцементными обшивками.
Исходные данные для расчета панелей (рис.6)
Обшивки
крепятся к алюминиевому каркасу на винтах М6х200 001 (оцинкованные) с
шагом 200 мм. Обшивки толщиной
=
=
10 мм. Перекрываемый пролет 300 см.
Влажность внутри помещения равна 75 %.
Расчет напряжений в элементах панели
А. Подсчет нагрузок
Расчет производится для IV ветрового района (Москва и Московская обл.). Согласно СНиП 2.01.07 – 85 для данного района нормативная ветровая нагрузка составит 0,55 кН/м2 для стен высотой до 10 м над поверхностью земли.
Рис. 6. Схема поперечного сечения панели
1 – алюминиевый каркас; 2 – асбестоцементные обшивки
Коэффициент перегрузки равен 1,2, т.е. расчетная ветровая нагрузка будет равна 0,55· 1,2 = 0,66 кН/м2 . Так как ширина панели равна 1,2 м, то погонная нагрузка, приходящаяся на одно ребро, составит:
=
0,6·
0,55 = 0,33
кН/м;
=
0,6·
0,66 =
0,4 кН/м.
Б. Подсчет усилий М и Q
кН·
м;
кН.
В. Подсчет геометрических характеристик панели (рис. 7)
Собственный
момент инерции алюминиевого каркаса равен
=
67,64 см4
с площадью поперечного сечения, равной
=
4,16 см2
.
В
соответствии с [п. 4.3] определим расчетное поперечное сечение b
1
=
18
= 18 см +
; b
2
=
25
= 25
см +
,
где
=
2,5 см, a
=
=
1 см.
Определим положение нейтральной оси по формуле [24]:
отношение
=
0,1972, так как
=
7,1·
104
МПа;
см.
Моменты инерции ребра каркаса и обшивок и статические моменты обшивок относительно нейтральной оси будут:
=
67,64 + 4,16(
6 – 5,4428)2
=
68,93 см4
;
= 0,1972[20,5·
13
/12
+ 0,5(11,5 – 5,4428)2
]
=
148,
66 см4
;
=
0,19
72[27,5·
13
/12
+ 27,5(5,4428 – 0,5)2
] =
132,943
см4
;
=
68,93 + 147,66 + 132,943 =
350,533 см4
;
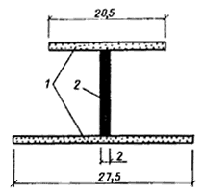
Рис. 7. Расчетное сечение панели
1 – асбестоцементная обшивка; 2 – алюминиевый каркас
20,5(11,5 – 5,4428)0,1972 = 24,487 см3
;
27,5(5,4428 – 0,5)0,1972 = 26,796 см3
.
По
формуле 22 определяем коэффициент податливости. Для этого по графику
на [черт. 3, кривая 2] определяем величину
=
21·
10-5
.
В соответствии с[п. 4.7]
=
1;
(
высота алюминиевого ребра) = 10 см;
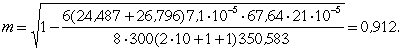
По формуле [23] определим
Следовательно,
для расчета каркаса принимаем т
=
= 0,198, для расчета обшивок принимаем т =
0,912.
Определяем положение нейтральной оси в соответствии с [п. 4.4] по формуле [18] с учетом податливости соединений обшивок с ребрами каркаса. Для расчета каркаса принят т = 0,198, следовательно:
см.
Моменты инерции относительно нового положения нейтральной оси будут равны:
=
67,64 + 4,16(6 – 5,75)2
= 67,9 см2
;
= 0,1972[20,5·
l3
/12
+ 20,5(11,5 – 5,75)2
] = 133,995 см4
;
= 0,1972[
27,5·
13
/12
+ 27,5(5,75 – 0,5)2
] = 149,92 см4
.
Для расчета обшивок принят m = 0,912. Определяем положение нейтральной оси при данном коэффициенте податливости:
см.
Моменты инерции каркаса и обшивок будут равны:
=
67,64 + 4,16(6 – 5,459)2
= 68,86 см4
;
=
0,1972[
20,5·
13
/12
+ 20,5(11,5 – 5,459)2
] = 147,87 см4
;
= 0,1972[27,5·
l3
/12
+ 27,5(5,459 – 0,5)2
] = 133,813 см4
;
Г. Определение напряжения в обшивках и в ребре каркаса
По
формулам [11] и [12] определяем напряжения в обшивках. Для этого по
формуле [19] определим коэффициент
при т
=
0,912
Напряжения в верхней сжатой обшивке будут равны:
МПа.
Напряжения в нижней растянутой обшивке будут равны:
МПа.
По
формуле [13] определяем напряжения в ребре каркаса. Для этого по
формуле [19] определим коэффициент
при т
=
0,198
В растянутой зоне ребра каркаса
МПа.
В сжатой зоне ребра каркаса
МПа.
Определим касательные напряжения в нейтральном сечении:
=
67,9 + 133,995 + 149,92 = 351,815 см4
;
=
0,1972·
27,5(5,75
– 0,5) =
28,47 см3
;
=
0,6·
28,47/0,2·
351,815
= 0,24 МПа.
Проверка прочности элементов панели
А Определение расчетных сопротивлений
элементов панели
Так
как длительно действующие и постоянные нагрузки в направлении,
перпендикулярном плоскости панели, отсутствуют, то согласно [п. 3.2а]
коэффициент условия работы панели равен 1. Согласно [п. 3.2б]
коэффициент условия работы панели для помещений с мокрым и влажным
режимом
=
0,8.
Следовательно, как было определено в первом примере:
=
30,5·
0,8 = 24,5
МПа;
= 8,5·
0,8 = 6,8
Мпа
и
= 13,5·
0,8 =
10,8 МПа.
Расчетное
сопротивление алюминия марки АМцМ термически неупрочняемой
= 40 МПа,
= 25 МПа.
Б. Проверка прочности
В
обшивках
= 1,75 МПа <
=
24,4 МПа;
=
1,46 МПа <
=
6,8 МПа.
В ребре каркаса:
в сжатой зоне
=
29,7 МПа <
=
40 МПа;
в растянутой зоне
=
26,9 МПа <
= 40 МПа;
=
0,24 МПа <
= 25 МПа.
Определение усилий, передаваемых на соединения обшивок с каркасом
По
формуле [25]
определим усилие
,
передаваемое на одну связь:
.
Максимальное усилие на связь будет осуществляться в начальный период эксплуатации, когда реализуется коэффициент податливости т = 0,912:
=
0,1972·
20,5(11,5
– 5,459) =
24,42 см3
;
=
0,1972·
27,5(5,459
–
0,5) =
26,89 см3
.
В нижней обшивке
0,912· 26,89· 45000/8· 5· 303,15 = 91 H.
В верхней обшивке
0,912· 24,42· 45000/8· 5· 303,15 = 83 H.
По
формулам [64] и [66] определим расчетные сопротивления,
воспринимаемые связями,
= 30 МПа, согласно СНиП II–23–81*
=
130 МПа.
По формуле [ 64]
= 0,25·
0,2·
0,6·
30·
1
02
= 90 H.
По формуле [66]
= 0,25
d2
=
0,25·
3,14·
0,62
·
130·
10-1
= 3,68 кН.
Принимаем
наименьшее значение усилия, полученного по формуле [64]
.
Таким образом, левая часть формулы [25] равна правой ее части,
полученной по формуле [64]
, т.е. 91Н
90Н.
Определение прогиба панели
Максимальный прогиб панели в середине пролета от равномерно распределенной нагрузки определим с учетом жесткости на изгиб, определенной по формуле [56] с коэффициентом податливости m = 0,198:
[67,9
+ 0,1982
(133,995 + 149,92)]
7,1·
104
=561,12
мПа·
см4
;
см,
т.е. прогиб составляет 1/665l , что допустимо, так как в соответствии с [ п. 4.24] допустимый прогиб стеновых панелей промышленных зданий должен быть равен или меньше(1/200 ).
Проверим жесткость панели при m = 0,912:
=
[68,86 + 0,9122
(147,87 + 133,813)]7
,1·
104
= 2152,35·
104
МПа·
см4
;
см,
что co ставляет(1/255)l .
ПРИМЕР 6 . РАСЧЕТ ЭКСТРУЗИОННОЙ СТЕНОВОЙ ПАНЕЛИ
Исходные данные для расчета панели
Панель,
поперечное сечение которой показано на рис. 8, предназначается для
наружного стенового ограждения производственного здания в Ровенской
обл. (III
район по скоростному напору
ветра, т.е.
=
0,45 кН/м2
).
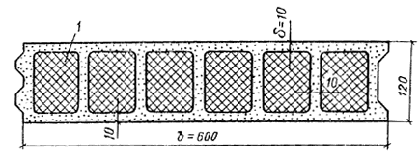
Рис. 8. Поперечное сечение экструзионной панели
1 – утеплитель
Длина панели 6 м; расчетный пролет панели с учетом [п. 6.17] равен 5,92 м. Панели проектируются как навесная конструкция, крепление панели к несущему каркасу в соответствии с (п. 6.15) обеспечивает свободу ее температурно–влажностных деформаций; панель опирается по коротким сторонам.
Здание
сооружается на открытой местности, имеет высоту до 10 м, имеет
открывающиеся проемы (двери, ворота, окна). Влажностный режим
помещения – нормальный:
=65%
;
температура помещения принимается:
в
холодное время года
=
130
С, в теплое время года – равной среднемесячной
температуре наружного воздуха в июле месяце.Панель удовлетворяет
требованиям ТУ 21–24–82–81. Панель изготавливается
по безавтоклавной технологии; предел прочности при изгибе (ТУ
21–24–82–81) экструзионного асбестоцемента не менее
18 МПа. Наружная поверхность панели покрашена краской, защищающей
асбестоцемент от увлажнения капельной влагой.
В соответствии с [пп. 1.4 – 1.7] производим расчет стеновой панели по несущей способности и деформациям на действие ветровых нагрузок, влажностных и температурных воздействий, действующих в процессе эксплуатации.
Расчет панели на действие ветровых нагрузок
А. Подсчет нагрузок
Нормативные
и расчетные
значения ветровых нагрузок, полученные по СНиП 2.01.07 – 85 с
учетом исходных данных, составляют: при положительном давлении ветра
= 0,45 кН/м2
и
=
0,54 кН/м2
; при отрицательном давлении ветра –
=
0,36 кН/м2
и
=
0,43 кН/м2
.
Б. Расчет напряжений в элементах панели
Расчет напряжений в элементах панели производится по [п. 4.12] и формулам [26] и [27].
Усилия М и Q определяем, учитывая частое расположение ребер (см. рис. 6) и соотношение размеров панели (ширина : длина = 1 : 10), а также заданное свободное опирание панели по коротким сторонам, в предположении работы панели по балочной схеме по формулам: М = 0,125ql 2 ; Q = 0,5ql .
Определяя
необходимые для расчета геометрические показатели, получим: I
=
4126·
10-8
м4
; S
=
417,5·
10-6
м3
;
=
7·
0,01 = 0,07
м; по [п. 6.17] l
=
6
– 0,08 = 5,92 м; по [п. 4.12]
h
=
0,12 м,
=
1.
В результате получим следующие значения напряжений:
при положительном давлении ветра
в полках
МПа;
в ребрах
МПа;
мПа;
при отрицательном давлении ветра
= ± 1,65 МПа;
=
±
1,37 МПа;
=
0,11 МПа.
В. Расчет прогиба панели
Расчет прогиба панели производим по формуле:
Определяем
по формуле [56] жесткость на изгиб панели D
,
принимая по [п. 3.3] и [табл. 4] значение
=
11·
103
МПа:
D = 11· 103 · 4126· 10-8 = 45386· 10-2 кН· м2 и получаем следующие значения прогиба панели:
при положительном давлении ветра
f = 5· 0,45· 0,6· 5,924 /384· 45386· 102 = 0,95· 10-2 м
(прогиб в сторону помещения);
при отрицательном давлении ветра
f = 0,76· 10-2 м (прогиб в сторону "улицы").
Расчет панели на влажностные воздействия
Расчет панели производится по указаниям [пп. 4.16, 4.17, 4.19, 4.29].
При
расчете панели, как следует из [п. 4.17], нужно предварительно
определить нормативные и расчетные значения влажностных деформаций
полок
панели.
А. Определение влажностных деформаций элементов панели
Определение
влажностных деформаций производится, как следует из [п. 4.17], только
для полок панели. Значения
определяются в соответствии с [п. 4.19] по данным о значениях
W
о
и
W
к
.
Значение W о принимается для экструзионного асбестоцемента по [п. 4.19]: W о = 3,5 %.
Значение
W
к
материала наружной полки панели определяем по (табл. 6)
для всех указанных в ней видов влажностных воздействий. Необходимые
для определения W
к
от воздушного увлажнения (высушивания) материала значения
и
найдем по данным СНиП 2.01.01 – 82 "Строительная
климатология и геофизика": для г. Ровно
=
99 %,
== 76 %. Значения W
к
,
соответствующие значениям
и
,
определяем по [
черт. 9, кривая 2
]
:
W
к
=
8,5 % и W
к
=
3,5%.
Для
случая увлажнения наружной полки панели капельной влагой [табл. 6]
W
к
=
20 %.
Значение конечной влажности W
к
материала внутренней полки, соответствующее заданному значению
= 65 %, определяем по [черт. 9]
: W
к
=
2,8%.
По
полученным выше зачениям W
к
и принятому значению W
о
= 3,5 % определяем по [п. 3.7] и [черт. 1, кривая 2]
нормативные значения влажностных деформаций
и
,
вызванные изменением влажности экструзионного асбестоцемента от
W
о
до W
к
.
При этом в соответствии с [п. 3.7], учитывая исходные данные о
наличии защитной покраски наружной поверхности панели, значения
,
для случая увлажнения наружной полки капельной влагой, следует
умножать на коэффициент 0,75.
Расчетные
значения
и
определяются в соответствии с [п. 4.19] умножением нормативных
значений на 1,1.
Результаты
подсчета значений
и
приведены в табл. 7.
Б. Расчет влажностных напряжений в элементах панели и прогибов панели
Расчет напряжений в элементах панели и прогибов панели производим по [пп. 4.16, 4.17, 4.29] и формулам [36]– [39] и [60] при следующих показателях:
и
– принимаем по табл. 7;
=
= 0 – по [п. 4.17];
=
==11·
103
МПа;
=
=
0,6·
0,01
= 60·
10-4
м;
=
7·
0,1·
0,01
= 70·
10-4
м;
=
= 0,6·
0,055 =
330·
10-6
м;
= (70 + 60 + 60)·
10-4
= 190·
10-4
м.
В
соответствии с [черт. 8] при
,
=
–0,175 и
=
0,175.
Определим влажностные напряжения и прогибы панели для одного из реальных случаев влажностных воздействий на панель (см. табл. 6): сочетание одновременного увлажнения наружной полки капельной влагой и воздушного высушивания внутренней полки панели.
Таблица 7
|
Элемент панели |
Вид влажностного воздействия |
Влажность материала, % по массе |
Значения
|
||
|
|
|
начальная |
конечная |
нормативные |
расчетные |
|
|
Воздушное увлажнение |
3,5 |
8,5 |
|
|
|
Наружная полка |
Воздушное высушива–ние |
3,5 |
3,5 |
0 |
0 |
|
|
Увлажнение капельной влагой |
3,5 |
2 |
|
|
|
Внутренняя полка |
Воздушное высушива–ние |
3,5 |
2,8 |
|
|
Расчетные усилия N
и М
,
возникающие от влажностных
воздействий, получим по формулам [41] и [42], подставляя
соответствующие значения
=
0,062 % и
= 0,0138% (см. табл. 7):
11·
103
·
60·
10-4
(0,062
– 0,0138) = 31810 H;
11·
103
·
330·
10-6
(0,062
+ 0,0138) = 2751,5 Н·
м.
Подставляя значения М и N в формулы [36] и [39], получим следующие значения напряжений:
в наружной полке
МПа;
во внутренней полке
МПа;
в ребре со стороны наружной полки
МПа;
в ребре со стороны внутренней полки
МПа.
Расчет
прогиба панели производим по [п. 4.29], подставляя значения М
,
подсчитанные по формуле [41] для нормативных значений
и
(см. табл. 7), в формулу [60]:
= 11·
103
·
330·
10-6
(0,056
+ 0,0125) = 2486,6 Н·
м;
м.
Аналогичным образом производится расчет панели на другие виды возможных [см. табл. 6] влажностных воздействий (воздушное увлажнение наружной поверхности панели, воздушное высушивание внутренней поверхности панели, сочетание этих воздействий), которые, как показывает анализ, вызывают меньшие напряжения и прогибы, чем полученные выше значения.
Расчет панели на температурные воздействия
Расчет
панели производится по [п. 4.16 – 4.18]. При расчете по [п.
4.17] нужно определить нормативные и расчетные значения температурных
деформаций элементов панели: полок
и
и ребер
и
панели.
А Определение температурных деформаций элементов панели
Определение
температурных деформаций элементов панели производится по формулам
[43] – [48], по данным
и
,
и
.
Значения
и
принимаем для г. Ровно по СНиП
2.01.07–85:
=26°С (июль месяц) и
=
24°С.
Значения и принимаются в соответствии с исходными данными: = 20 °С (среднемесячная июльская температура), = 13 °С.
Необходимое для расчета значение принимается по [4.18] равным 17 °С.
Значения для экструзионного асбестоцемента принимается по [п. 3.6] и [табл. 5]; при этом учитывая, что наружная поверхность панели защищена от увлажнения капельной влагой, а максимальная влажность от воздушного увлажнения не превышает [черт. 9, кривая 2] 8,5 %, принимаем значение [табл. 5] для температур 0 °С и ниже при W < 12 %, тогда = 1,1· 10-5 для всего диапазона температур.
Пользуясь полученными данными, подсчитаем нормативную величину температурных деформаций наружной полки для холодного времени года с помощью формул [43] и [47]:
%.
Проведем аналогичным образом подсчет нормативных и расчетных значений деформаций элементов панели и , и , необходимых для расчета температурных напряжений по формулам [36] – [39]; результаты приведены в табл. 8.
Б. Расчет температурных напряжений в элементах панели и прогибов панели
Расчет напряжений в элементах панели и прогибов панели производится по формулам [36] – [39] и [60]. Однако с учетом [п. 4.12] ограничимся расчетом только температурных прогибов экструзионной панели.
Расчет прогиба панели производится по [п. 4.29]. Определим прогиб панели от температурных воздействий, действующих в холодное время года.
Определяем по формуле [41] значение М при нормативных значениях температурных деформаций и , и , из табл. 8:
= 11· 103 · 330· 10-6 [(– 0,045 %)+0,0044 %] + 0,5[(–0,045)(–0,175) + (–0,0044)0,175]11· 103 · 70· 10-4 · 0,1 = – 1 200 ,1 Н· м.
Тогда по формуле (60) имеем:
м (прогиб в сторону помещения).
Определяем аналогичным образом прогиб панели от температурных воздействий, действующих в теплое время года:
м (прогиб в сторону "улицы").
Проверка прочности элементов панели и прогиба панели
В соответствии с требованиями СНиП 2.01.07 – 85 проверку прочности элементов и прогиба панели производим на действие наиболее неблагоприятного сочетания нагрузок и воздействий (с учетом возможного отсутствия некоторых из них).
А. Проверка прочности элементов панели
Определим по данным расчета панели, приведенным в табл. 9, значения неблагоприятных напряжений, возникающих в элементах панели от действия отдельных нагрузок и их основных сочетаний, и проведем проверку прочности элементов по формулам [1] – [4]. При этом в соответствии с [п. 3.1] принимаем расчетные сопротивления экструзионного асбестоцемента R [табл. 3] при значении предела прочности, равном 18 МПа/см2 ; в соответствии с [п. 3.2] умножаем значения R материала наружной полки, учитывая наличие водонепроницаемой краски, на = 0,9; в соответствии с СНиП 2.01.07 – 85 умножаем суммарные напряжения на коэффициент = 0,9. Результаты проверки прочности элементов панели приведены в табл. 9.
Таким образом, из табл. 9 следует, что напряжения в элементах панели не превышают значения расчетных сопротивлений.
Таблица 8
|
Время года |
Темпера тура на ружного воздуха среднесу точная |
Темпера тура внут реннего воздуха помеще ния |
Элемент панели |
Значение изменения температуры элемента панели , |
Значение температурных деформаций элемента панели и |
||
|
|
|
|
|
норма тивное |
расчет ное |
норма тивное |
расчет ное |
|
Теплое время года |
= 26 о C |
= 20 о C |
Наружная полка и примыкающее к ней во локно ребра |
= 9 °С |
= = 9,9°С |
= = = 0,01% |
= = = 0,011% |
|
|
|
|
Внутренняя полка и примыкащее к ней волокно ребра |
= 3°С |
= = 3,3 °С |
= = = 0,0036% |
= = = 0,004% |
|
Холодное время года |
= -24 о C |
= 13 о C |
Наружная полка и примыкающее к ней волокно ребра |
= = -41 °С |
= = -45,1 °С |
= = - 0,045% |
= = = –0,05% |
|
|
|
|
Внут ренняя полка и примыкающее к ней волокно ребра |
= – 4 °С |
= – 4,4°С |
= = –0,0044% |
= = – 0,005% |
Таблица 9
|
Элемент панели, месторасположение волокна по сечению панели |
Нормальные и касательные напряжения, МПа, от действия |
Значения неблагоприятных напряжений и , в том числе суммарных напряжений |
Расчетные сопротивле ния материала R, МПа |
Проверка прочности элемента по формулам [ 1] –[ 4] |
|||
|
|
ветровой нагрузки при давлении |
влаж ност–ных |
, МПа |
|
|
||
|
|
поло жи тель ном |
отрица тель ном |
воз дейст вий |
|
|
|
|
|
Полка |
крайнее волокно наружной полки |
= – 2 |
= = 1,65 |
= = – 14 |
= 1,65 = – 3,14 · 0,9 = = – 2,83 |
= 6 · 0,9 = = 5,4 =23 · 0,9 = 20,7 |
1,65 < < 5,4; 2,82 < 20,7 |
|
Пол ка |
крайнее волокно внутренней полки |
= 2 |
= = – 1,65 |
= = – 0,81 |
= 2 = – 2 ,46 · 0,9 = = – 2,16 |
= 6 =23 |
2 < 6; 2,46 < < 23 |
|
Ребро |
волокно, примыкаю шее к на–полке |
= = – 1,72 |
= = 1,37 |
= = 5, 01 |
= – 1,72 = 6,38 · 0,9 = = 5,7 4 |
= 12 |
5,74< < 12 |
|
Ребро |
волокно, примыкав шее к вну ренней полке |
= = 1,72 |
= = – 1,37 |
= = – 1,66 |
= 1,72 = – 3,02 · 0,9 = = – 2,73 |
= 6 =23 |
1,72<6; 2,73< < 23 |
|
|
волокно по нейтральной оси |
= = 0,139 |
= = 0,11 |
|
= 0,139 |
= 12 |
0,139< < 3,5 |
Б. Проверка прогиба панели
Проверка прогиба панели производится по [п. 4.24].
Как показывает анализ полученных выше данных о прогибах панели, наибольший прогиб в сторону помещения вызывает сочетание положительного ветрового давления и температурных воздействий в холодное время года f = 0,95· 10-2 + 1,16· 10-2 = 2,11· 10-2 м, а наибольший прогиб панели в сторону "улицы" вызывает сочетание, включающее одновременное действие отрицательного давления ветра, увлажнения наружной поверхности и воздушного высушивания внутренней поверхности панели и температурного нагрева наружной поверхности панели f = (0,76 + 2,39 + 0,18)10-2 = 3,33· 10-2 м.
Таким образом, максимальное значение прогиба панели с учетом коэффициента сочетания нагрузок = 0,9 составляет f = 3,33· 10-2 · 0,9 = 3· 10-2 м, что с допустимой точностью удовлетворяет требованиям [п. 4.24], в соответствии с которым величина предельного прогиба стеновой панели для промышленных зданий составляет по [табл. 7] (l/200)l , т.е. 2,96· 10-2 м.
ПРИМЕР 7. РАСЧЕТ БЕСКАРКАСНОЙ СТЕНОВОЙ ПАНЕЛИ
Панель, поперечное сечение которой показано на рис. 9, предназначается для наружного ограждения стен производственного здания в IV районе по скоростному напору ветра.
Панель проектируется как навесная конструкция, опирающаяся по коротким сторонам.
Рис. 9. Поперечное сечение панели
1 – доска (обрамление); 2 – асбестоцементные обшивки; 3 – клеевой шов; 4 – заполнитель (пенопласт)
Исходные данные для расчета панели
Длина панели – 3 м, расчетный пролет панели с учетом [п. 6.17] равен 2,9 м. Здание сооружается на местности типа А и имеет высоту до 10 м. Панель располагается с наветренной стороны в здании с температурой воздуха t = 17 °С и нормальным влажностным режимом помещения. Обшивки 1 панели выполнены из плоского прессованного асбестоцементного листа; предел прочности асбестоцемента при изгибе –23 МПа. Наружная поверхность панели не защищена от увлажнения. Заполнитель панели выполнен из пенопласта марки ПСБ плотностью 40 кг/м3 .
Расчет напряжений в элементах панели
Расчет напряжений в элементах панели производим по [п. 4.13] .
Определяя с учетом исходных данных нормативные и расчетные значения ветровых нагрузок по СНиП 2.01.07 – 85, получим:
= 0,55· 1· 0,8 = 0,44 кН/м2 ;
= 0,44· 1,4 = 0,61 кН/м2 .
Определяя в соответствии с [п. 4.13] при = момент инерции сечения панели, получим:
= 1,18· 0,008(0,06 + 0,008)2 /2 = 21,8· 10-6 м4 .
В результате, определяя максимальные напряжения в элементах панели по формулам [28] – [30], получим:
в обшивках
===±( 0,61· 1,18· 2,922 · 0,038/8· 21,6· 10-6 ) =
= ± 1,318 МПа;
в заполнителе
=
= 0,61· 1,18· 2,9/(2· 0,06 + 0,008 + 0,008)· 1,12 = 0,0137 МПа.
Проверка прочности элементов панели
Проверку прочности элементов панели производим по формулам [1], [2], [7].
Для определения значений расчетных сопротивлении R материала асбестоцементного листа в соответствии с [п. 3.1] исходное значение предела прочности материала, равное 23 МПа, умножаем на коэффициент 0,9, получая в результате величину предела прочности, равную 23 МПа0,9 = 20 МПа, по которой в [табл. 1] находим значение R . При этом по [п. 3.2] умножаем значение R для увлажняемой наружной сжатой обшивки, учитывая отсутствие влагозащитной покраски, на = 0,8. Тогда получим = 30,5· 0,8 = 24,4 МПа, = 8,5 МПа.
В соответствии с [табл. 1 прил. 2] принимаем расчетное сопротивление пенопласта сдвигу = 0,04 МПа.
В результате проверки прочности элементов панели получим:
< = 24,4 МПа; < = 8,5 МПа; < = 0,04 МПа.
Расчет и проверка прогиба панели
Расчет прогиба панели производим по формуле:
Определяя D по [п. 4.28], принимаем значение модуля сдвига пенопласта ПСБ = 40 кг/м3 по [табл. 1 прил. 1] = 2,2 МПа, значение модуля упругости Е асбестоцемента – по [табл. 2]: Е = 14· 103 МПа.
Тогда, по формуле [59] получим:
=14000· 21,8· 10-6 /2,97 =102,7 кН· м2 .
Подсчитаем прогиб панели:
f= 0,013· 0,45· 1,18· 2,94 /102,7 = 0,46· 10-2 м.
Предельный прогиб панели, определяемый по [п. 4.24], составляет:
(1/200)l = (1/200)2,9 = 1,45· 10-2 м.
Проведя проверку прогиба панели, получим:
0,46· 10-2 < 1,45· 10-2 .
ПРИМЕР 8. РАСЧЕТ СТОЙКИ ИЗ ЭКСТРУЗИОННОГО ШВЕЛЛЕРА
Исходные данные для расчета элемента
Центрально–сжатая стойка является составным элементом подстропильной конструкции холодной чердачной крыши жилого дома (рис. 10). Внутреннее помещение чердака сообщается с наружной атмосферой через слуховые окна.
Рис. 10. Поперечный разрез крыши
1 – асбестоцементные листы; 2 – обрешетка; 3 – стропила; 4 – стойка подстропильной конструкции; 5 – чердачное перекрытие
Стойка выполнена из асбестоцементного экструзионного швеллера N° 28 (рис. 11) с площадью поперечного сечения = 57,24· 10-4 м2 и минимальным моментом инерции сечения = 233,6· 10-8 м4 . Предел прочности экструзионного асбестоцемента при изгибе (ТУ 21–24–82 – 81) не менее 16 МПа. Закрепление концов стойки шарнирное, расстояние между центрами закреплений – 2 м. Расчетная сжимающая нагрузка N = 18 кН. В местах закрепления сечение стойки ослаблено четырьмя отверстиями для болтов d = 16 мм. Защита подстропильной конструкции от увлажнения отсутствует.
Расчет напряжений в стойке
Расчет напряжений в центрально–сжатых экструзионных конструкциях следует определять по формуле [52] и п. 4.14. Определяя гибкость асбестоцементной стойки с учетом [п. 4.22], получим:
.
По графику [черт. 10] находим: при = 94 = 0,27.
Рис. 11. Поперечное сечение стойки
При расчете на устойчивость определяем напряжения в стойке по формуле [52]:
18000/0,27· 57,24· 10-4 = 11,7 МПа.
При расчете на прочность с учетом ослаблений определяем напряжения в стойке по п. 4.14.
1 8000/(57,24 – 4· 1,6· 1,4)10-4 = 3,72 МПа.
Проверка устойчивости и прочности стойки
Проверка устойчивости и прочности стойки производится по формуле [6].
определяется по [табл. 3], при временном сопротивлении изгибу экструзионного асбестоцемента, равном 16 МПа, = 21 МПа.
При заданных условиях эксплуатации в соответствии с [ п. 3.2], умножаем на коэффициент условий работы = 0,65.
Проведя проверку устойчивости стойки, получим
= 11,7 МПа < = 21· 0,65 = 13,65 МПа.
Проведя проверку прочности стойки, получим
= 3,72 МПа < = 13,65 МПа.
Таким образом, прочность и устойчивость стойки обеспечена.
ПРИМЕР 9. РАСЧЕТ ЭКСТРУЗИОННОЙ ПЛИТЫ ДЛЯ БЕЗРУЛОННОЙ КРОВЛИ
Исходные данные для расчета плиты
Асбестоцементная экструзионная плита (рис. 12) предназначена для устройства двухскатной безрулонной крыши сельского жилого дома с уклоном ската кровли –14° (рис. 13). Плиты соединены в коньке шарнирным зажимом, а в карнизе упираются в мауэрлатный элемент через соединительные изделия, входящие в зацепление с нижней полкой плит. Нормативный снеговой покров в районе строительства – 1500 Па. Масса 1 м плиты – 330 Па. Предел прочности при изгибе материала плиты – 20 МПа. Наружная поверхность экструзионной плиты защищена кремнийорганической жидкостью 136–41 (ГОСТ 10834 – 76*). Плита имеет следующие геометрические показатели: ]