СНиП II-22-81 (1995), часть 2

• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6

3.12. Расчетные сопротивления сжатию кладки из крупных пустотелых бетонных блоков различных типов устанавливаются по экспериментальным данным. При отсутствии таких данных расчетные сопротивления следует принимать по табл. 4 с коэффициентами:

0,9 при пустотности блоков £ 5 %

0,5 « « « £ 25 «

0,25 « « « £ 45 «

где процент пустотности определяется по среднему горизонтальному сечению.

Для промежуточных значений процента пустотности указанные коэффициенты следует определять интерполяцией.

3.13. Расчетные сопротивления сжатию кладки из природного камня, указанные в табл. 4, 5 и 7, следует принимать с коэффициентами:

0,8 — для кладки из камней получистой тески (выступы до 10 мм);

0,7 — для кладки из камней грубой тески (выступы до 20 мм).

3.14. Расчетные сопротивления сжатию кладки из сырцового кирпича и грунтовых камней следует принимать по табл. 7 с коэффициентами:

0,7 — для кладки наружных стен в зонах с сухим климатом;

0,5 — то же, в прочих зонах;

0,8 — для кладки внутренних стен.

Сырцовый кирпич и грунтовые камни разрешается применять только для стен зданий с предполагаемым сроком службы не более 25 лет.

3.15. Расчетные сопротивления кладки из сплошных камней на цементно-известковых, цементно-глиняных и известковых растворах осевому растяжению R_t , растяжению при изгибе R_tb и главным растягивающим напряжениям при изгибе R_tw , срезу R_sq при расчете сечений кладки, проходящих по горизонтальным и вертикальным швам, приведены в табл. 10.

Таблица 10

3.16. Расчетные сопротивления кладки из кирпича и камней правильной формы осевому растяжению R_t , растяжению при изгибе R_tb , срезу R_sq и главным растягивающим напряжениям при изгибе R_tw при расчете кладки по перевязанному сечению, проходящему по кирпичу или камню, приведены в табл. 11.

Таблица 11

3.17. Расчетные сопротивления бутобетона осевому растяжению R_t , главным растягивающим напряжениям R_tw и растяжению при изгибе R_tb приведены в табл. 12.

Таблица 12

Рис. 1. Растяжение кладки по неперевязанному сечению

Рис. 2. Растяжение кладки по перевязанному сечению

Рис. 3. Растяжение — кладки при изгибе по перевязанному сечению

3.18. Расчетные сопротивления кладки из природного камня для всех видов напряженного состояния допускается уточнять по специальным указаниям, составленным на основе экспериментальных исследований и утвержденным в установленном порядке.

3.19. Расчетные сопротивления арматуры R_s , принимаемые в соответствии с главой СНиП по проектированию бетонных и железобетонных конструкций, следует умножать в зависимости от вида армирования конструкций на коэффициенты условий работы g _cs , приведенные в табл. 13.

Таблица 13

МОДУЛИ УПРУГОСТИ И ДЕФОРМАЦИЙ КЛАДКИ ПРИ КРАТКОВРЕМЕННОЙ И ДЛИТЕЛЬНОЙ НАГРУЗКЕ, УПРУГИЕ ХАРАКТЕРИСТИКИ КЛАДКИ, ДЕФОРМАЦИИ УСАДКИ, КОЭФФИЦИЕНТЫ ЛИНЕЙНОГО РАСШИРЕНИЯ И ТРЕНИЯ

3.20 . Модуль упругости (начальный модуль деформаций) кладки Е₀ при кратковременной нагрузке должен приниматься равным: для неармированной кладки

Е₀ = a R_u ; (1)

для кладки с продольным армированием

Е₀ = a R_sku . (2)

В формулах (1)и (2) a  — упругая характеристика кладки, принимается по п. 3.21.

Модуль упругости кладки с сетчатым армированием принимается таким же, как для неармированной кладки.

Для кладки с продольным армированием упругую характеристику следует принимать такой же, как для неармированной кладки; R_u  — временное сопротивление (средний предел прочности) сжатию кладки, определяемое по формуле

R_u = kR, (3)

где k  — коэффициент, принимаемый по табл. 14:

R — расчетные сопротивления сжатию кладки, принимаемые по табл. 2 — 9 с учетом коэффициентов, приведенных в примечаниях к этим таблицам, а также в пп. 3.9 — 3.14.

Таблица 14

Упругую характеристику кладки с сетчатым армированием следует определять по формуле

(4)

В формулах (2) и (4) R_sku  — временное сопротивление (средний предел прочности) сжатию армированной кладки из кирпича или камней при высоте ряда не более 150 мм, определяемое по формулам:

для кладки с продольной арматурой

; (5)

для кладки с сетчатой арматурой

(6)

m  — процент армирования кладки;

для кладки с продольной арматурой

m =

где А_s и А_k  — соответственно площади сечения арматуры и кладки, для кладки с сетчатой арматурой m определяется по п. 4.30;

R_sn  — нормативные сопротивления арматуры в армированной кладке, принимаемые для сталей классов А-I и А-II в соответствии с главой СНиП по проектированию бетонных и железобетонных конструкций, а для стали класса Вр-I — с коэффициентом условий работы 0,6 по той же главе СНиП.

3.21 . Значения упругой характеристики a для неармированной кладки следует принимать по табл. 15.

Таблица 15

3.22. Модуль деформаций кладки Е должен приниматься:

а) при расчете конструкций по прочности кладки для определения усилий в кладке, рассматриваемой в предельном состоянии сжатия при условии, что деформации кладки определяются совместной работой с элементами конструкций из других материалов (для определения усилий в затяжках сводов, в слоях сжатых многослойных сечений, усилий, вызываемых температурными деформациями, при расчете кладки над рандбалками или под распределительными поясами) по формуле

Е= 0,5 e ₀ , (7)

где, e ₀ — модуль упругости (начальный модуль деформаций) кладки, определяемый по формулам (1) и (2).

б) при определении деформаций кладки от продольных или поперечных сил, усилий в статически неопределимых рамных системах, в которых элементы конструкций из кладки работают совместно с элементами из других материалов, периода колебаний каменных конструкций, жесткости конструкций по формуле

Е= 0,8 e ₀ , (8)

3.23. Относительная деформация кладки с учетом ползучести определяется по формуле

e = v (9)

где s — напряжение, при котором определяется e ;

n  — коэффициент, учитывающий влияние ползучести кладки;

v = 1,8   для кладки из керамических камней с вертикальными щелевидными пустотами (высота камня 138 мм);

v = 2,2   для кладки из глиняного кирпича пластического и полусухого прессования;

v = 2,8 — для кладки из крупных блоков или камней, изготовленных из тяжелого бетона;

v = 3,0 — для кладки из силикатного кирпича и камней полнотелых и пустотелых, а также из камней, изготовленных из бетона на пористых заполнителях или поризованного и силикатных крупных блоков:

v = 3,5 — для кладки из мелких и крупных блоков, изготовленных из автоклавного ячеистого бетона вида А;

v = 4,0 — то же, из автоклавного ячеистого бетона вида Б.

3.24. Модуль упругости кладки Е₀ при постоянной и длительной нагрузке с учетом ползучести следует уменьшать путем деления его на коэффициент ползучести v .

3.25. Модуль упругости и деформаций кладки из природных камней допускается принимать по специальным указаниям, составленным на основе результатов экспериментальных исследований и утвержденным госстроями союзных республик в установленном порядке.

3.26. Деформации усадки кладки из глиняного кирпича и керамических камней не учитываются.

Деформации усадки следует принимать для кладок:

из кирпича, камней, мелких и крупных блоков, изготовленных на силикатном или цементном вяжущем, — 3× 10^-4 ;

из камней и блоков, изготовленных из автоклавного ячеистого бетона (вида А), — 4× 10^-4 ;

то же, из неавтоклавного ячеистого бетона (вида Б) — 8× 10^-4 ;

3.27. Модуль сдвига кладки следует принимать равным G = 0,4 Е₀ , где Е₀  — модуль упругости при сжатии.

3.28. Величины коэффициентов линейного расширения кладки следует принимать по табл. 16.

Таблица16

3.29. Коэффициент трения следует принимать по табл. 17.

Таблица 17

4. РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ПЕРВОЙ ГРУППЫ (ПО НЕСУЩЕЙ СПОСОБНОСТИ)

КАМЕННЫЕ КОНСТРУКЦИИ

Центрально-сжатые элементы

4.1. Расчет элементов неармированных каменных конструкций при центральном сжатии следует производить по формуле

N £ т_g j RA, (10)

где, N — расчетная продольная сила;

R — расчетное сопротивление сжатию кладки, определяемое по табл. 2 — 9;

j  — коэффициент продольного изгиба, определяемый по п. 4.2;

а — площадь сечения элемента;

т — коэффициент, учитывающий влияние длительной нагрузки и определяемый по формуле (16) при е_0g = 0.

При меньшем размере прямоугольного поперечного сечения элементов h ³ 30 см (или с меньшим радиусом инерции элементов любого сечения i ³ 8,7 см) коэффициент т_g следует принимать равным единице.

4.2. Коэффициент продольного изгиба j для элементов постоянного по длине сечения следует принимать по табл. 18 в зависимости от гибкости элемента

(11)

или прямоугольного сплошного сечения при отношении

(12)

и упругой характеристики кладки a , принимаемый по табл. 15, а для кладки с сетчатым армированием — по формуле (4).

В формулах (11) и (12):

l₀  — расчетная высота (длина) элемента, определяемая согласно указаниям п. 4.3;

i — наименьший радиус инерции сечения элемента;

h — меньший размер прямоугольного сечения.

Таблица 18

Рис. 4. Коэффициенты j и т_g по высоте сжатых стен и столбов

а - шарнирно опертых на неподвижные опоры; б - защемленных внизу и имеющих верхнюю упругую опору; в - свободно стоящих

4.3. Расчетные высоты стен и столбов l₀ при определении коэффициентов продольного изгиба j в зависимости от условий опирания их на горизонтальные опоры следует принимать:

а) при неподвижных шарнирных опорах l₀ = Н (рис. 4,а);

б) при упругой верхней опоре и жестком защемлении в нижней опоре: для однопролетных зданий l₀ = 1, 5H, для многопролетных зданий l₀ = 1, 25H (рис. 4,б);

в) для свободно стоящих конструкций l₀ = 2Н (рис. 4,в);

г) для конструкций с частично защемленными опорными сечениями — с учетом фактической степени защемления, но не менее l₀ = 0,8Н, где Н — расстояние между перекрытиями или другими горизонтальными опорами, при железобетонных горизонтальных опорах расстояние между ними в свету.

Примечания: 1. При жестких опорах (см. п. 6.7) и заделке в стены сборных железобетонных перекрытий принимается l₀ = 0, 9H , а при монолитных железобетонных перекрытиях, опираемых на стены по четырем сторонам, l₀ = 0,8H .

2. Если нагрузкой является только собственная масса элемента в пределах рассчитываемого участка, то расчетную высоту l₀ сжатых элементов, указанную в п. 4.3, следует уменьшить путем умножения на коэффициент 0,75.

4.4. Значения коэффициентов j и т_g для стен и столбов, опирающихся на шарнирные неподвижные опоры, с расчетной высотой l₀ = Н (см. п. 4.3) при расчете сечений, расположенных в средней трети высоты l₀ следует принимать постоянными, равными расчетным значениям j и т_g , определенным для данного элемента. При расчете сечений на участках в крайних третях l₀ коэффициенты j и т_g увеличиваются по линейному закону до единицы на опоре (рис. 4,а).

Для стен и столбов, имеющих нижнюю защемленную и верхнюю упругую опоры, при расчете сечений нижней части стены или столба до высоты 0,7 Н принимаются расчетные значения j и т_g , а при расчете сечений верхней части стены или столба значения j и т_g для этих сечений увеличиваются до единицы по линейному закону (рис. 4,б).

Для свободно стоящих стен и столбов при расчете сечений в их нижней части (до высоты 0,5Н) принимаются расчетные значения j и т_g , а в верхней половине значения j и т_g увеличиваются до единицы по линейному закону (рис. 4,в).

В месте пересечения продольной и поперечной стен, при условии их надежного взаимного соединения, коэффициенты j и т_g разрешается принимать равными 1. На расстоянии Н от пересечения стен коэффициенты j и т_g определяются по пп. 4.1 — 4.3. Для промежуточных вертикальных участков коэффициенты j и т_g принимаются по интерполяции.

4.5. В стенах, ослабленных проемами, при расчете простенков коэффициент j принимается по гибкости стены.

Для узких простенков, ширина которых меньше толщины стены, производится также расчет простенка в плоскости стены, при этом расчетная высота простенка принимается равной высоте проема.

4.6. Для ступенчатых стен и столбов, верхняя часть которых имеет меньшее поперечное сечение, коэффициенты j и т_g определяются:

а) при опирании стен (столбов) на неподвижные шарнирные опоры — по высоте l₀ = Н (Н — высота стены или столба согласно п. 4.3) и наименьшему сечению, расположенному в средней трети высоты Н ;

б) при упругой верхней опоре или при ее отсутствии — по расчетной высоте l₀ , определенной согласно п. 4.3, и сечению у нижней опоры, а при расчете верхнего участка стены (столба) высотой Н₁ — по расчетной высоте l_{0 1} и поперечному сечению этого участка; l_{0 1} определяется так же, как l₀ , но при Н = Н₁ .

Внецентренно сжатые элементы

4.7. Расчет внецентренно сжатых неармированных элементов каменных конструкций следует производить по формуле

N £ т_g j ₁ RA_c w, (13)

где А_c  — площадь сжатой части сечения при прямоугольной эпюре напряжений (рис. 5), определяемая из условия, что ее центр тяжести совпадает с точкой приложения расчетной продольной силы N. Положение границы площади А_c определяется из условия равенства нулю статического момента этой площади относительно ее центра тяжести для прямоугольного сечения

А_c = A, (14)

j ₁ = (15)

В формулах (13)   (15):

R — расчетное сопротивление кладки сжатию;

A — площадь сечения элемента;

h — высота сечения в плоскости действия изгибающего момента;

e₀  — эксцентриситет расчетной силы N относительно центра тяжести сечения;

j  — коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый по расчетной высоте элемента l₀ (см. пп. 4.2, 4.3) по табл. 18;

j _c  — коэффициент продольного изгиба для сжатой части сечения, определяемый по фактической высоте элемента Н по табл. 18 в плоскости действия изгибающего момента при отношении

или гибкости

,

где h_c и i_c  — высота и радиус инерции сжатой части поперечного сечения А_c в плоскости действия изгибающего момента.

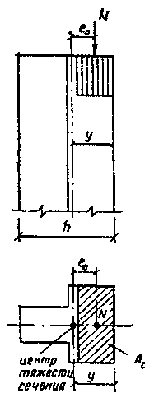
Рис. 5. Внецентренное сжатие

Рис. 6. Знакопеременная эпюра изгибающего момента для внецентренно сжатого элемента

Для прямоугольного сечения h_c = h — 2e₀ . Для таврового сечения (при e₀ > 0,45y ) допускается приближенно принимать А_c = 2(у - e₀ )b и h _с = 2(у - e₀ ), где у — расстояние от центра тяжести сечения элемента до его края в сторону эксцентриситета; b — ширина сжатой полки или толщина стенки таврового сечения в зависимости от направления эксцентриситета.

При знакопеременной эпюре изгибающего момента по высоте элемента (рис. 6) расчет по прочности следует производить в сечениях с максимальными изгибающими моментами различных знаков. Коэффициент продольного изгиба j _c следует определять по высоте части элемента в пределах однозначной эпюры изгибающего момента при отношениях или гибкостях

• часть 1
• часть 2
• часть 3
• часть 4
• часть 5
• часть 6