Проектир. самонапряж. ЖБК (к СНиП 2.03.01-84), часть 3

• часть 1
• часть 2
• часть 3
• часть 4

Из рассмотренных вариантов сечения балки и ее армирования наиболее экономичными и легкими являются профили следующих балок: h = 0,8 м и b = 5 см при бетоне класса В 60, h = 0,9 м и b = 4 см при бетоне класса В60 и h = 1 м и b = 4 см при бетоне класса В50 (черт. 3).

Черт. 3. Варианты сечения двутавровой самонапряженной балки с механическим напряжением продольной арматуры

Учитывая совокупность показателей стоимости и массы рассмотренных вариантов балки, а также возможность изготовления конструкций с тонкими стенками (например, при бетонировании балки в горизонтальном положении), целесообразно выбрать балку высотой h = 1 м, толщиной стенки b = 4 см из бетона класса В50 при стоимости материалов балки 39 и 32,9 руб. в зависимости от вида арматуры. В этом случае масса балки будет равна 2,28 т, расход металла на балку с продольной арматурой из стали марки 20ХГ2Ц составит 174 кг, а из высокопрочной проволоки ¾ 65 кг.

Расчет выбранного сечения балки по предельным состояниям первой группы при стержневом армировании

Прочность выбранного сечения балки определяем по формуле (16') рекомендуемого приложения 3:

Имеем: a_sp = 6 см; a'_sp = 97 см; yh = 15 см;

R_bt,ser = 225 МПа; R¢ _s = 1030 Мпа;

см² ; см² ;

N = 0 ; кН.

Рассматриваем вариант нагружения балки вскоре после изготовления, когда потери еще мало проявились:

МПа;

N¢ _sp = 2,75(48, 6 - 40 ) = 2,75 × 8,6 = 23,5 кН;

N'f = 0,6 × 225 = 540 кН.

Подставляя значения в формулу (16') рекомендуемого приложения 3, получим

М = 554(1 - 0,02) + 23,5(1 - 0,97) - 540(0,075 - 0,02) =

= 543 + 0,7 - 30,5 = 513,2 кН × м > 504 кН × м,

при этом по формуле (16) рекомендуемого приложения 3

см (т. е. меньше высоты свесов).

Находим координату центра тяжести:

Проверяем условие (17) рекомендуемого приложения 3 при x =

Для принятых относительных характеристик

'

что и должно быть, поскольку при расчете по трещиностойкости не допускалось перенапряжение в сжатой зоне балки.

Расчет главных растягивающих и сжимающих напряжений при нормативной нагрузке

Главные растягивающие и сжимающие напряжения определяются в сечении, находящемся на расстоянии 1 м от опоры, где обычно заканчивается уширение стенки балки над опорой, а наименьшая величина h = 4 см предельно приближена к опоре. Нормативная нагрузка на опору кН.

Для установления марки бетона по самонапряжению и степени армирования тонкой стенки балки производим ее расчет по трещиностойкости и по прочности в относительных единицах.

Находим площадь и момент инерции сечения балки по формулам (18) и (19) при s _о = 0,6:

Статический момент сечения определяется для любой точки на расстоянии х от верха балки в обобщенном виде по формуле (20) рекомендуемого приложения 3:

По заданным размерам для точек, находящихся на центральной оси балки при х = 1 — d _o , получим

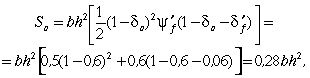
а у места примыкания стенки к верхней полке балки при х = 0,15

S_v = bh² [ 0,15 ( - 0,6) ² + 0,6 (1 - 0,6 - 0,06)] = 0,225 bh₂ .

Определяем приближенно нормальные напряжения на оси центра тяжести балки у опоры по формуле (21) рекомендуемого положения 3 при h = 1 м, b = 4 см и бетоне класса В50:

см² ;

МПа.

В зоне примыкания к верхней полке s _by = 0.

Находим касательные напряжения t _o и t_g на этих участках:

МПа;

МПа.

Для определения главных напряжений на этих участках находим самонапряжение, задаваясь маркой напрягающего бетона. Пользуясь табл. 3 и формулами (1) ¾ (3) настоящего Пособия, находим

где

При использовании стержневой арматуры при m + m¢ - 0,017 k_m = 1,3; при использовании проволочной арматуры при m + m¢ = 0,0073 k_m = 0,83. Для двухосного армирования k_s = 1,2.

Коэффициент k_e можно принять равным единице. Тогда при использовании стержневой арматуры

s _bp = 2 × 1, 3 × 2 × 1 = 3,1 МПа;

при использовании проволочной арматуры

s _bp = 2 × 0,83 × 1,2 × 1 = 2 МПа.

Главные напряжения по формуле (23) рекомендуемого приложения 3 при использовании стержневой арматуры будут равны:

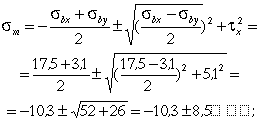
s _mc = - 18 ,8 МПа < 28 МПа;

s _mt = - 1,8 МПа < 3 МПа.

Главные напряжения по формуле (23) рекомендуемого приложения 3 при использовании высокопрочной арматурной проволоки будут равны:

s _mc = 18,45 МПа < 28 МПа;

s _mt = - 1,05 МПа < 3 МПа.

Определяем необходимое сечение А _sx поперечной арматуры:

при стержневой арматуре

см² или 7 Æ 8 мм;

при высокопрочной арматурной проволоке

см² или 5 Æ 6 мм.

Самонапряжение s _sx в арматуре А _sx соответственно равно:

МПа; МПа.

Определяем потери самонапряжения от усадки и ползучести бетона. При влажности 0,7 для напрягающего бетона марки S _р 2,5 по табл. 4 настоящего Пособия имеем полную усадку Î ₈ = 74 × 10^-5 . Поправка на переменность режима и двухосное ограничение деформации дает усадку

Î ₈ = 74 × 10^-5 × 0,8 × 0,6 = 48 × 10^-5 .

Ползучесть бетона для балок с подобным армированием, когда исключено какое-либо перенапряжение крайних фибр балки, не превышает 60 × 10^-5 . Суммарная деформация составит

Î ₈ + Î ⁹ = (48 + 60)10^-5 = 108 × 10^-5 . Потери напряжения в арматуре составят

Ds _s = 108 × 10^-5 × 2 × 10⁶ = 216 МПа.

Дополнительное растягивающее усилие в арматуре от самонапряжения при коэффициенте армирования m = 0,017 составит

МПа £ 216 МПа.

Самонапряжение почти полностью компенсирует потери напряжения в арматуре балки.

Пример 4. Расчет покрытия базисного склада завода тяжелых транспортных машин на резиновом ходу.

Покрытие склада представляет собой армобетонную неразрезную плиту толщиной h, лежащую на упругом основании (грунте), на которую действует широко расставленная сосредоточенная нагрузка от колес стоящей или движущейся транспортной машины, вызывающая изгибающие моменты М = 28 кН × м и М = 21 кН × м. Кроме того, при изменении температуры окружающего воздуха свободные концы плиты покрытия длиной в каждую сторону 40 м удлиняются или укорачиваются, скользя по гравийно-щебеночному основанию, в результате чего в средней части покрытия возникают сжимающие или растягивающие усилия.

Принимая предварительную толщину плиты h = 21 см, коэффициент трения между плитой и основанием m = 0,5, получим предельное усилие, возникающее в средней части покрытия как результат охлаждения плиты на 30 °С:

N = 0,21 × 25 × 0,5 × 40 = 105 кН.

Перемещение концов плиты при этом составит 10^-5 × 30 × 40 × 10³ = 12 см.

Расчетные усилия при коэффициенте перегрузки n = 1,2 составят:

M_crc = 28 × 1,2 = 33,4 кН × м; N_crc = 105 × 1,2 = 126 кН;

M¢ _{cr c} = 21 × 1,2 = 26 кН × м; N¢ _crc = 126 кН.

Для плиты покрытия:

F = F' = 0,29; В = В' = 0,67; 5 = = 0,5; d _N = d¢ _N = 0,5;

d _sp = 0 , 12 ; d¢ _sp = 0,88; y¢ _f = 0 .

Подставляя указанные значения в формулы (4) — (7) рекомендуемого приложения 3, получим:

D = (0,67 - 0,12) (0,67 - 1 + 0,88) - (0,67 - 0,88) (0,67 - 1 + 0,12) = 0,258;

q = 0,29 (0,67 - 1 + 0,88) - 0,29 (0,67 - 0,88) + 0,22;

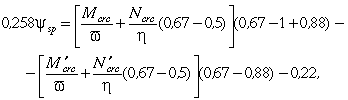
откуда

Подставляя величины y _sp и y¢ _sp в уравнение (8) рекомендуемого приложения 3, получим:

Подставляя величины М и N получим

откуда

Принимаем напрягающий бетон класса В70 с расчетным сопротивлением по прочности на осевое растяжение для предельного состояния второй группы R_{bt , ser} = 3,3 МПа, марка бетона по самонапряжению S_p 2.

Учитывая, что покрытие будет вводиться в эксплуатацию не ранее 3 мес, в соответствии с рекомендациями п. 2.5 вводим коэффициент 1,3, тогда

s _bt,ser = 1,3 × 3,3 = 4,2 МПа.

Находим самонапряжение бетона s _{b р} при двухосном армировании m = 0,002, пользуясь табл. 2 и формулами (1) ¾ (3) настоящего Пособия:

где

тогда

Подставляя величины R_bt,ser и R_bp , получим:

Находим мультипликаторы и в общем виде:

= bh² R_bt,ser = 1000h² × 4,2 = 4200h² кН × м;

h = bhR_bt,ser = 1000h × 4,2 = 4200 h кН.

Подставляя мультипликаторы и h , получим:

h² - 0,016h - 0,022 = 0.

Определяем оптимальную высоту сечения h :

Принимаем толщину плиты h = 16 см.

Мультипликаторы v и h будут иметь следующие значения:

v = 1000 × 160² × 4,2 = 107 кН × м;

h = 1000 × 160 × 4,2 = 670 кН.

Подсчитываем относительные величины усилий y _sp и y¢ _sp в арматуре:

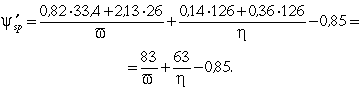
Подставляя значения v и h , получим:

Определяем усилия в арматуре при нулевом напряжении в бетоне:

Nsp = y _sp h = 0,11 × 670 = 74 кН;

N¢ _sp = y¢ _sp h = 0,02 × 670 = 13 кН.

Определяем необходимую площадь арматуры класса A-IV по формуле (10) рекомендуемого приложения 3:

Определяем значение s _b8 .

Для района расположения завода в восточной зоне минимальная влажность воздуха j = 70 %. Тогда по табл. 4 настоящего Пособия для бетона марки S _р 2 при двухосном армировании и переменном влажностном режиме усадка составит

Î ₈ = 0,8 × 0,6 × 74 × 10^-5 = 38 × 10^-5 .

Потери напряжения от ползучести по расчетам составят

Î ₉ = 50 × 10^-5 .

Полные потери напряжения от усадки и ползучести составят

Ds _sp = ( Î ₈ + Î ₉ ) E_s = (38 + 50) 10 ^-5 × 2 × 10 ⁶ = 176 МПа.

Находим площадь арматуры:

% .

Прямым подбором получено экономичное, характерное для армобетона сечение плиты покрытия.

Пример 5. Расчет напорной самонапряженной трубы диаметром 7,5 м.

Напорные самонапряженные трубы предназначены для трубопроводов диаметром 7,5 м ГАЭС, длиной 600 м с разностью отметок между бассейнами 100 м, рассчитанных на рабочее давление 1,6 МПа.

Конструкция трубы представляет собой (черт. 4) самонапряженный трубчатый сердечник 9, спирально обвитый канатной арматурой 6 , которая защищена от повреждений или коррозии толстым слоем самонапряженного железобетона 5 толщиной 80 мм. Сердечник армируется арматурным каркасом 1, а защитный слой ¾ сеткой 7 . Полигон для производства самонапряженных труб располагает формами, позволяющими получать трубы со стенкой толщиной 330 и 400 мм. Трубы предназначены для укладки в траншею с засыпкой на высоту 2 м над шелыгой.

Для напрягающего бетона напорных труб большого диаметра применяем свойственный напрягающему бетону высокий класс прочности на осевое растяжение B_t 4,8, которому по табл. 2 настоящего Пособия соответствует сопротивление R_bt,ser = 3 ,7 МПа. Учитывая, что трубопровод будет вводиться в эксплуатацию после полугодия со дня изготовления труб, вводим, согласно рекомендациям п. 2.5 настоящего Пособия, повышающий коэффициент 1.4, тогда

R_bt,ser = 1,4 × 3,7 = 5,2 МПа.

Рассматриваем два типоразмера напорных самонапряженных труб со стенками толщиной:

I типоразмер — 250 + 80 = 330 см;

(сердечник) (защитный слой)

II " 320 + 80 = 400 см.

(сердечник) (защитный слой)

В табл. 7 приведены коэффициенты к нагрузкам М и N (черт. 5), действующим на трубопровод в траншее на глубине Н над шелыгой.

Для расчета армирования трубы (см. черт. 4) предварительно напряженным канатом 11 и сварными сетками 1 и 7 имеем:

для трубы со стенкой толщиной h = 330 мм

r = 4,08 м ¾ внешний радиус;

r _о = 3,75 м ¾ внутренний радиус

D_f = 8 ,16 м ¾ внешний диаметр;

Н = 2,0 м ¾ земля над шелыгой;

для трубы со стенкой толщиной h = 400 мм

r = 4,15 м ¾ внешний радиус;

r _о = 3,75 м ¾ внутренний радиус;

D_f = 8,30м ¾ внешний диаметр;

Н = 2,0 м ¾ земля над шелыгой.

Для расчета величин нагрузок M_crc и N_crc на трубу диаметром 7,5 м пользуемся черт. 5, где приведены нагрузки на каждый из четырех участков трубопровода, на которые разбита линия трубопровода. В табл. 7 приведены нагрузки нижнего наиболее нагруженного участка трубопровода.

Таблица 7

Коэффициенты х и у к нагрузкам М и N

Усилие	Нагрузка от веса	Угол q , град			Формула	Результаты расчета для труб типоразмеров
		0	105	180		330	400
Коэффициент х
М,	Трубы	-0,07	+0,088	-0,122	xr (2,4 × 2 p rh )	828х	1039 х
кН × м	Земли	-0,067	+0,089	-0,126		1118х	1155x
	Воды	-0,07	+0,088	-0,122	xr (1,0 p rо 2 )	1802х	1833x
Коэффициент у
N,	Трубы	-0,061	+0,297	+0,207	у (2,4 × 2 p rh )	203у	250у
кН	Земли	+0,383	+0,539	+0,327		274у	278у
	Воды	-0,220	-0,062	-0,272	у (1,0 p rо 2 )	442у	42у

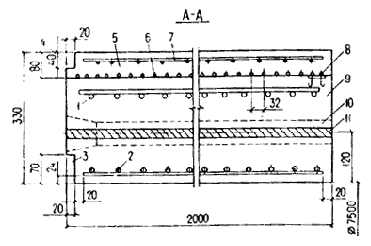
Черт. 4. Конструкция самонапряженной железобетонной трубы диаметром 7.5 м

1 ¾ внешний каркас; 2 ¾ внутренний каркас; 3 ¾ внутренний паз; 4 ¾ наружный паз; 5 ¾ защитный слой; 6 ¾ спиральная намотка; 7 ¾ арматурная сетка (конструктивная); 8 ¾ анкер намотки; 9 ¾ сердечник; 10 ¾ каналы; 11 ¾ продольные канаты

Нормативные и расчетные нагрузки на трубу приведены в табл. 8 и 9.

Таблица 8

Нагрузки на трубу со стенкой толщиной h = 330 мм

Сечение под углом q ,	От веса			От внут реннего давления	Итого нагрузки
град	трубы	земли	воды	Np =pr о b	нормативные	расчетные
Изгибающие моменты М, кН × м
0	58	-74,	-126,2	¾	-259	-28 5
105	+72,8	+99,5	+158,6	—	+331	+364
180	-101,1	-140,8	-219,9	¾	-462	-508
Нормальные усилия N, кН
0	-12,4	+104,9	-87,2	-6000	-6005	-6600
105	+60,3	+147,6	-27,4	-6000	-5820	-6490
180	+42,0	+89,6	-120,2	-6000	-5990	-6588

Таблица 9

Нагрузки на трубу со стенкой толщиной h = 400 мм

Сечение под углом q , град	Îò âåñà			От внут реннего давления	Итого нагрузки
	трубы	земли	воды	Np =pr о b	нормативные	расчетные
Изгибающие моменты М, кН × м
0	72	-77	-12 8	¾	278	-306
105	+91	+102	+161	¾	+355	+391
180	-126	-145	-223	¾	-496	-545
Нормальные усилия N, кН
0	-15	+106	-97	-6000	-6005	-6606
105	+74	+105	-27	-6000	-5803	-6383
180	+51	+91	-120	-6000	-5977	-6575

Подсчитываем значения мультипликаторов при расчетном сопротивлении напрягающего бетона R_bt,ser = 5,2 МПа для всех рассматриваемых значений h = 330 мм и h = 400 мм:

при h = 330 мм h = bhR_br,ser = 1000 × 330 × 5 ,2 = 1 716 000 H = 1716 кН;

v = bh² R_bt,ser = 1000 × 330² × 5 ,2 = 565 280 000 Н × мм = 566 кН × м;

Черт. 5. Суммарная эпюра изгибающих моментов в стенках трубы

при h = 400 мм h = 1000 × 400 × 5,2 = 2 080 000 H = 2080 кН;

v = 1000 × 400 ² 5,2 = 832 000 000 Н × мм = 832 кН × м.

Для одновременного действия двух систем нагрузок М _crc и N_crc , M¢ _crc и N ¢ _crc используем формулы (4') — (7') рекомендуемого приложения 3. Для труб со стенкой толщиной h = 330 мм и Р = 1,6 МПа имеем:

F= F ¢ = 0,20; В = В' = 0,67; d _N = d¢ _N = 0,5;

q = 180^о ; М_crc = 508 кН × м; N_crc = 6588 кН;

q = 105^о ; М ¢ _crc = 364 кН × м; N ¢ _crc = 6491 кН;

h = 1716 кН; v = 566 кН × м.

По формулам (6') и (7') рекомендуемого приложения 3:

D = (0,67 - 0,12) (0,67   1 + 1,12)   (0,67   1,12) (0,67   1 + 0,12) = 0,34;

q = 0,29(0,67   l + l,12)   0,29(0,67   l,12) = 0,36.

Подставляем значения в формулы (4') и (5') рекомендуемого приложения 3:

Учитывая целесообразность передачи главного усилия от давления воды 1,6 МПа на предварительно напрягаемую спиральную обмотку, расцениваем ее в виде усилия N_sp = 6000 кН (102 витка каната класса К-7, Æ 9 мм), прибавляем и вычитаем из выражения y _sp величину ,

тогда

Разбиваем это уравнение на два:

(для арматурных сеток);

(для каната).

Подставляем для y _{s р} значения h и v :

что дает для арматуры в сетке

N_sp = y _sp1 h = 0,67 × 1716 = 1150 кН.

Следовательно, площадь рабочей арматуры в сетке из стержней Æ 16 мм из стали класса А-1 при расчетном ее сопротивлении растяжению для предельного состояния второй группы R_s,ser = 235 мПа составит

Принимаем армирование из 29 Æ 16 мм, класса А-1.

Армирование защитного слоя определяется по формуле (4') рекомендуемого приложения 3:

или

откуда y¢ _sp1 = 0,04,

т.е. расчетная арматура в защитном слое не требуется. Армируем защитный слой конструктивной сеткой из проволоки Æ 4 мм.

Для труб со стенками толщиной h = 400 мм и Р= 1,6 МПа y _sp для арматурных сеток равен:

Необходимо также задаться числом витков арматуры и усилием, воспринимающим внутреннее давление. Рассмотрим случай, когда сохранены 102 витка каната класса К-7, Æ 9 мм и, следовательно, N_sp = 6 000 кН. Тогда имеем расчетное уравнение для арматурной сетки

Подставляя значения h и v , получим

т.е. расчетная арматура в сердечнике не требуется.

Перед проектировщиком возникают возможности либо армировать сердечник легкой проволочной сеткой, либо уменьшить число витков обмотки и получить расчетное армирование сердечника.

Представленный порядок расчета целесообразно с технологических позиций выполнить для остальных участков трубопровода, меняя лишь число витков каната класса К-7, Æ 9 мм.

Целесообразно при расчете трубы со стенкой толщиной h = 4 00 мм ориентироваться на сетку с расчетной арматурой из стержней диаметром 12 мм того же класса А-1.

Такие расчеты рекомендуется выполнять самим для овладения приемами прямого метода расчета.

ПРИЛОЖЕНИЕ 3

Рекомендуемое

ПРЯМОЙ МЕТОД РАСЧЕТА САМОНАПРЯЖЕННЫХ КОНСТРУКЦИЙ

1. ОБЩИЕ ПОЛОЖЕНИЯ

В СНиП 2.03.01-84 не приводятся рекомендации по предварительному назначению геометрических характеристик сечений конструкций, класса бетона, вида, количества и расположения арматуры, величины ее предварительного напряжения.

Для многих, особенно сборных железобетонных, конструкций выбор оптимальных размеров конструкции, ее формы, высоты, ширины и т. д. опытному проектировщику не составляет больших трудностей, и можно ожидать, что заданные или принятые им размеры будут оптимальны по весу (расходу бетона), по затратам металла и стоимости.

Однако на деле, особенно в монолитном и сборно-монолитном строительстве, для самонапряженных и для сочетания самонапряженных с механическим предварительным напряжением объектов (конструкций или сооружений), во-первых, всегда действуют две системы нагрузок М, N и М¹ , N¹ или М и М¹ разных знаков; во-вторых, существует самонапряжение в одном, двух и трех направлениях. Естественно, выбрать заранее оптимальные размеры проектируемого объекта практически невозможно. Для этой цели в помощь проектировщикам в „Инструкции по проектированию самонапряженных железобетонных конструкций" (СН 511-78), утвержденной Госстроем СССР в 1978 г., наряду с традиционным методом был изложен прямой метод расчета конструкций в относительных единицах всех действующих параметров при двух системах нагрузок М, N и М¹ , N ¹ , позволяющий, не задаваясь для объекта величинами характеристик сечения, ожидаемых потерь напряжений и используя метод разделения переменных, найти окончательные уравнения путем составления матриц различных возможных решений (конкретных размеров объекта и его армирования).

Эти матрицы с точки зрения затраты металла, расхода бетона или стоимости позволяют выбрать окончательные параметры для рассматриваемого объекта (размеры сечений и армирование).

Выбрав размеры объекта по таким показателям и учитывая требования СНиП 2.03.01-84, необходимо произвести проверку параметров объектов по предельным состояниям первой группы.

Конструкции и сооружения, для которых особенно полезен такой подход, включают:

все большепролетные сборные железобетонные конструкции;

протяженные сооружения покрытий дорог, аэродромов, производственных площадей, полов зданий;

трубы гидротехнических и мелиоративных сооружений;

сооружения промышленного, гражданского и транспортного назначения;

резервуары для воды и светлых нефтепродуктов;

вертикальные стволы шахт;

различные стержневые статически неопределимые системы и т.д.

Таким образом, рекомендации изложенного прямого метода расчета оптимальных параметров рассчитываемого объекта позволяют проектировщику заложить оптимальные параметры объекта при расчете самонапряженных и предварительно напряженных конструкций и сооружений в соответствии со СНиП 2.03.01-84.

Самонапряженные конструкции являются разновидностью предварительно напряженных железобетонных конструкций. Особенностью самонапряженных конструкций является напряжение всей расположенной в бетоне арматуры независимо от ее направления. Величина напряжений в арматуре и бетоне, возникающих в процессе расширения бетона совместно с заанкеренной в нем арматурой, зависит от технологических и конструктивных факторов (количества арматуры, расположения ее в сечении ¾ симметричного, несимметричного, в двух или трех направлениях, дополнительных силовых или упругих связей примыкания к ñìåæíûì конструкциям, трения по основанию и т. п.).

Конструктивная форма, вид армирования и характер нагружения современных конструкций и сооружений настолько усложнились, что, применяя самонапряженный железобетон, а в некоторых случаях ¾ одновременно и механическое преднапряжение арматуры, приходится прибегать в расчетах подобных конструкций к постепенному приближению оптимальных высоты, ширины и класса бетона, выполнению многократных пересчетов, что чрезвычайно громоздко и трудоемко.

В связи с этим особое значение приобретают практические методы проектирования и расчета, позволяющие находить оптимальные сечения бетона и арматуры, в том числе при воздействии эксплуатационных, монтажных или других нагрузок, вызывающих в конструкциях внутренние усилия и напряжения другого знака.

Рекомендуемый прямой метод расчета позволяет подбирать сечения предварительно напряженных и самонапряженных конструкций одновременно с учетом этих двух различных воздействий.

Противоположные по знаку усилия могут возникать в различных участках конструкции и при одном воздействии (например, в стенке напорной трубы, в шелыге и боковых участках), в покрытиях дорог и аэродромов, неразрезных заводских площадях и полах (под сосредоточенной нагрузкой и на некотором расстоянии) и в других случаях, но армировать такие конструкции нужно постоянно по всей длине с обеих сторон.

Применяется метод разделения переменных характеристик на две группы: 1-я ¾ изменяющиеся, т.е. требующие определения расчетом, и 2-я ¾ принятые в расчете неизменными и назначаемые по правилам разд. 2 настоящего приложения в виде относительных величин. В качестве изменяющихся характеристик обычно рассматриваются b, h, R_bt.ser , А _s и А ¢ _s .

При расчете самонапряженных конструкций прямым методом необходимо руководствоваться следующими положениями:

1. Подбор сечения производится на расчетные внутренние усилия в конструкции М и N и противоположного знака М¹ и N¹ усилие может иметь тот же знак).

2. В основу расчета положено основное напряженном состояние конструкции при действии условных внешних сил М_о , N _о и М ¢ _о , N¢ _o , создающих в сечении треугольную эпюру напряжений (черт. 1). В этом случае усилия в арматуре известны:

N _о = A_s s _sp ; N¢ _o = A_s s¢ _sp , (1)

где обычно при использовании стали одной марки для арматуры A_s и A¢ _s s _sp = s¢ _sp .

Черт. 1. Îñíîâíîå напряженное состояние конструкции при действии условных внутренних сил М_о , N _о и М ¢ _о , N¢ _o

3. Любое сложное поперечное сечение элемента рассматривается в обобщенном виде (черт. 2), при этом его прямоугольная часть bh является основой конструкции, принятой за единицу; d _f (I   d¢ _f ) , d _sp , d¢ _sp ¾ отношение расстояний от точек приложения усилий, действующих соответственно в уширениях, свесах и арматуре, до низа самонапряженной конструкции к высоте сечения. Эти характеристики показаны на черт. 3 для общего случая предварительного напряжения, когда в сечении имеется и ненапряженная арматура. Для самонапряженных конструкций y _s , y ' _s , d _s и d¢ _s равны нулю.

4. Для характеристики сопротивления бетонного сечения действию растяжения и изгиба вводятся мультипликаторы h и v рассчитываемой конструкции:

h = bhR_bt,ser ; v = hh = bh ² R_bt,ser , (2)

с помощью которых усилия в арматуре N_sp и N¢ _sp выражаются в относительных величинах y _sp и y ' _sp , которые определяются по формулам

и (3)

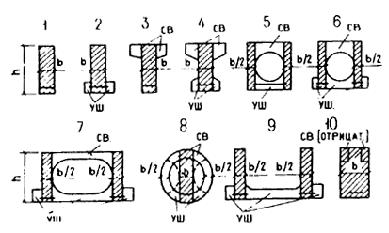
Черт. 2. Различные формы поперечного сечения изгибаемых предварительно напряженных конструкций, применяемых в промышленном и гражданском строительстве

1-10 ¾ варианты формы сечения; „св." и „уш." ¾ сокращенное обозначение свесов и уширений

Черт. 3. Относительные характеристики и напряженное состояние течения конструкции в стадии трещинообразования при действии усилий М _crc и N_crc от эксплуатационной нагрузки и М' _crc и N¢ _crc ¾ от эксплуатационной нагрузки другого знака или от монтажной нагрузки

Аналогично выражаются относительные характеристики y _{s р} и y¢ _f усилий, действующих в момент трещинообразования соответственно в свесах, уширениях, а также относительные характеристики y _N и y _b ¾ внешней продольной силы N_crc и суммы всех усилий растяжения N_sp + N¢ _sp + N_f .

Рассмотрение конструкции в обобщенном виде позволит прямым расчетом получить величины y _{s р} и y¢ _{s р} для нижней и верхней предварительно напряженной арматуры без назначения размеров сечения и прочности материалов конструкции, как это обычно принято делать.

5. Уравнения равновесия сил (знак „плюс" ¾ растяжение) составляются в относительных единицах:

(4)

(5)

где

(6)

(7)

где F , F¹ ¾ удельные сопротивления бетонных сечений в обобщенном виде с учетом свесов;

В, В¹ — относительные расстояния от места приложения равнодействующей всех сил сжатия от низа конструкции.

Величины F , F¹ и В, В¹ принимаются по табл. 1 прямого метода расчета.

6. Полученные (после подстановки величин известных нагрузок и относительных характеристик сечения) уравнения равновесия решаются в указанной ниже последовательности относительно высоты сечения h с использованием формул (2) настоящего приложения совместно с условием равномерного обжатия сечения

(8)

Из уравнений (4) и (5) настоящего приложения:

где x , у , z ¾ численные значения, полученные подстановкой заданных величин.

Подставив в уравнение (8) значения y _{s р} и y¢ _sp , получим общее уравнение

(9)

Таблица I

Коэффициенты F и В прямого метода расчета

g	Коэффициенты при y¢ f , равном В
	-0,1	0	0,1	0,2	0,3	0,4	0,6	1	2	4	8
0	0,221 0,584	0,292 0,676	0,340 0,732	0,372 0,773	0,395 0,803	0,413 0,827	0,436 0,862	0,462 0,903	¾	¾	0,500 1,000
0,05	0,229 0,592	0,292 0,676	0,334 0,727	0,362 0,764	0,382 0,729	0,397 0,814	0,419 0,846	0,441 0,884	0,461 0,926	¾	0,475 0,975
0,10	0,236 0,600	0,292 0,676	0,328 0,727	0,352 0,756	0,369 0,780	0,383 0,801	0,402 0,829	0,421 0,866	0,439 0,904	¾	0,450 0,950
0,15	0,240 0,607	0,292 0,676	0,323 0,716	0,343 0,747	0,358 0,769	0,369 0,788	0,386 0,814	0,403 0,847	0,418 0,883	0,425 0,907	0,427 0,925
0,20	0,242 0,615	0,292 0,676	0,317 0,711	0,335 0,739	0,347 0,759	0,357 0,776	0,370 0,799	0,385 0,829	0,398 0,861	0,404 0,884	0,406 0,912
0,30	0,245 0,628	0,292 0,676	0,308 0,702	0,320 0,723	0,328 0,740	0,334 0,751	0,343 0,769	0,352 0,791	0,360 0,819	0,364 0,837	0,366 0,850
0,40	0,245 0,640	0,292 0,676	0,300 0,695	0,308 0,709	0,312 0,723	0,316 0,729	0,320 0,741	0,324 0,759	0,327 0,777	0,328 0,792	0,330 0,800

Примечания: 1. Коэффициенты F ¹ и В¹ определяются по данной таблице с заменой на y¢ _f на y _f .

2. ¾ для сжатой зоны, имеющей свесы, полки и т.п.; ¾ для сжатой зоны прямоугольного сечения.

Подставив значения v и h в уравнение (9)получим

Решая уравнение как квадратное относительно h, находим оптимальную высоту изгибаемого сечения, отвечающую оптимальному размещению и величине армирования обеих зон конструкции и заданным нагрузкам.

7. По известным относительным усилиям в арматуре с помощью формулы (3) настоящего приложения определяется армирование обеих зон конструкции:

где R_s,ser  — расчетное сопротивление арматуры растяжению для предельных состояний второй группы;

s _s8 ¾ потери напряжений в арматуре;

g _sp ¾ коэффициент точности натяжения, принимаемый равным 0,9.

• часть 1
• часть 2
• часть 3
• часть 4